How to punch a hole in some 3D distribution of points

Question

Suppose we have a long list of 3D Cartesian coordinates, defining a distribution of random points in 3D space. How could we remove all the points inside a sphere of radius sphereRadius located at coordinates sphereLocation = {X, Y, Z}?

This Boolean subtraction is probably trivial, but I didn't found any useful info on how to do it with Mathematica 7.0. Maybe it isn't trivial, after all.

---

Generalisation : How can we do the same with an arbitrary closed surface, instead of a sphere, if the hole is defined as a deformed sphere ?

holeLocation = {X, Y, Z};
hole[theta_, phi_] = holeLocation  + 
    radius[theta, phi] {Sin[theta]Cos[phi], Sin[theta]Sin[phi], Cos[theta]};

where theta and phi are the usual spherical coordinates.

Answer 1

Using my solution to a similar question asked on StackOverflow some time ago,

Pick[dalist,UnitStep[criticalRadius^2-Total[(Transpose[dalist]-frameCenter)^2]],0]

which is for any number of (Euclidean) dimensions and should be quite fast.

EDIT

Ok, here is a generalization of the vectorized approach I proposed:

ClearAll[cutHole];
cutHole[relativeData_, holdRadiusF_] :=
  Module[{r, theta, phi, x, y, z},
    {x, y, z} = Transpose[relativeData];
    r = Sqrt[Total[relativeData^2, {2}]];
    theta = ArcCos[z/r];
    phi = ArcTan[x,y];
    Pick[relativeData, UnitStep[r - holdRadiusF[theta, phi]], 1]];

Here is an illustration:

data = RandomReal[6, {10^6, 3}];
holeLoc = {3, 3, 3};
relativeData = Transpose[ Transpose[data] - holeLoc];

Define some particular shape of the hole:

holeRad[theta_, phi_] := 1 + 4 Sqrt[Abs[Cos[theta]]]

Pick the points:

kept =cutHole[relativeData,holeRad];//AbsoluteTiming

(* {0.631836,Null}  *)

Visualize:

Show[{
  ListPointPlot3D[Cases[kept, {_, _, _?Positive}]], 
  SphericalPlot3D[
    holeRad[\[Theta], \[Phi]], {\[Theta], Pi/4, Pi/2}, {\[Phi], 0, 2 Pi}, 
    PlotStyle -> Directive[Orange, Specularity[White, 10]], Mesh -> None]}]

The main point here is that the filtering function is vectorized and therefore quite fast.

Answer 2

Because the question refers to points using both Cartesian coordinates $(x,y,z)$ and spherical coordinates $(\theta, \phi)$, we need to convert between them:

spherical[{x_, y_, z_}] := {ArcTan[z, Norm[{x, y}]], ArcTan[x, y]};

A point p is inside the "hole" when its distance from the origin (computed with Norm) is less than the value given by the function radius. For flexibility, I have included an optional argument threshold that multiplies the value of radius:

inside[p_, origin_, radius_, threshold_: 1] :=  
  threshold radius @ spherical @ (p - origin) >= Norm[p - origin];

Use this to Select the points inside the hole (or, by negating inside, to exclude them):

pointsInside = Select[points, inside[#, origin = {0, 0, 0}, radius] &];

(I have chosen an origin of {0,0,0} for this example to make it easy to plot the hole using SphericalPlot3D.)

---

Example

Let's define a hole to illustrate:

radius[{\[Theta]_, \[Phi]_}] := (1 + Cos[\[Theta]]^2) (1 + Sin[ \[Phi]]^2);

We will need some points:

points = RandomReal[NormalDistribution[0, 1], {3000, 3}];

For the illustration, let's plot all those points, distinguishing those inside the hole from those outside it:

pointPlot = Graphics3D[{Opacity[0.3], Gray, Point @ points, 
  PointSize[0.01], Red, Opacity[0.5], Point @ pointsInside, 
  Black, Opacity[1], Point @ origin}];

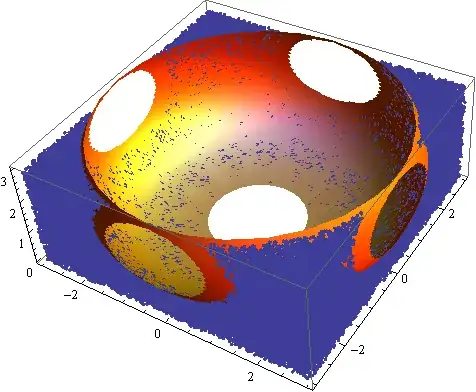
Here is the hole's boundary for reference:

hole = SphericalPlot3D[radius[{\[Theta], \[Phi]}], {\[Theta], 0, \[Pi]}, {\[Phi], 0, 2 \[Pi]},
 PlotStyle -> Opacity[0.25], Mesh -> None]

Put them together:

Show[pointPlot, hole]