8

I'm trying to convert to Mathematica a simple backward/forward sweep (with RK4 integrator) code to solve an optimal control problem in epidemiology, but I'm getting some error messages and I cannot identify where I'm coding wrong. The original code is written in MatLab and is in the reference "Maia Martcheva - An Introduction to Mathematical Epidemiology":

function ocmodel1
% This function computes the optimal control
% and the corresponding solution using forward-backward ...
sweep
clc;
clear all;

test = -1;

 Δ = 0.001; %set tolerance
 N = 100; %number of subdivisions
 h = 1/N; %step
 t = 0:h:1; % t-variable mesh


 u = zeros(1,length(t)); %initialization
 x = zeros(1,length(t));
 lam = zeros(1,length(t));

 x(1) = 10; %initial value assigned to x(0)

 beta = 0.05; %parameters
 mu = 0.01;
 gamma = 0.5;
 P = 100;
 w1 = 1;


 while (test<0) % while the tolerance is reached, repeat
 oldu = u;
 oldx = x;
 oldlam = lam;

for i=1:N %loop that solve the forward ...
differential equation
k1 = beta*(P-x(i))*x(i) -(mu + gamma)*x(i) - ...
u(i)*x(i);
k2 = beta*(P-x(i)-0.5*k1*h)*(x(i)+0.5*k1*h) - ...
(mu+gamma)*(x(i)+0.5*k1*h)...
-0.5*(u(i)+u(i+1))*(x(i)+0.5*k1*h);
k3 = beta*(P-x(i)-0.5*k2*h)*(x(i)+0.5*k2*h) - ...
(mu+gamma)*(x(i)+0.5*k2*h)...
-0.5*(u(i)+u(i+1))*(x(i)+0.5*k2*h);
k4 = beta*(P-x(i)-k3*h)*(x(i)+k3*h) - ...
(mu+gamma)*(x(i)+k3*h)...
-u(i+1)*(x(i)+k3*h);

x(i+1) = x(i) + (h/6)*(k1+2*k2+2*k3+k4);

end

for i=1:N %loop that solves the backward ...
differential equation of the adjoint system
j = N + 2 -i;
k1 = ...
-w1-lam(j)*(beta*(P-x(j))-beta*x(j)-(mu+gamma) ...
- u(j));
k2 = ...
-w1-(lam(j)-0.5*k1*h)*(beta*(P-x(j)+0.5*k1*h) ...
-(mu+gamma) -0.5*(u(j)+u(j-1)));
k3 = ...
-w1-(lam(j)-0.5*k2*h)*(beta*(P-x(j)+0.5*k2*h) ...
-(mu+gamma) -0.5*(u(j)+u(j-1)));
k4 = -w1 -(lam(j)-k3*h)*(beta*(P-x(j)+k3*h) ...
-(mu+gamma) - u(j-1));

lam(j-1) = lam(j) - (h/6)*(k1+2*k2+2*k3+k4);


end

u1 = min(100,max(0,lam.*x/2));
u = 0.5*(u1 + oldu);

temp1 = Δ *sum(abs(u)) - sum(abs(oldu - u));
temp2 = Δ *sum(abs(x)) - sum(abs(oldx - x));
temp3 = Δ *sum(abs(lam)) - sum(abs(oldlam -lam));

test = min(temp1,min(temp2,temp3));

end

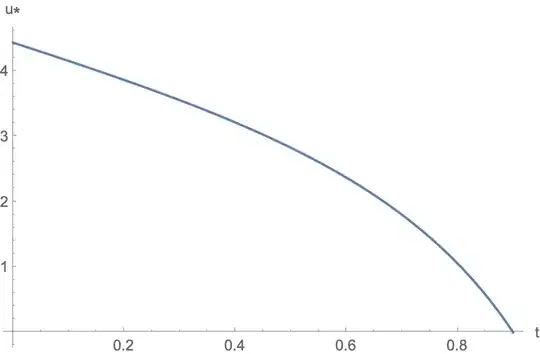
figure(1) %plotting
plot(t,u)


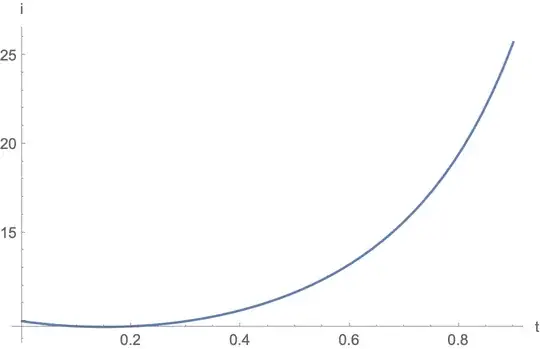
figure(2)
plot(t,x)

end

My attempt to write this code in Mathematica is in the following:

(* This function computes the optimal control
 % and the corresponding solution using forward-backward...
sweep *)
Clear[ all]
test = -1;
Δ = 0.001;
n = 100;
h = 1/n;
t = Range[0, 1, h];
u = {};
x = {};
lam = {};
For[i = 1, i < n,
 AppendTo[u, 0];
 AppendTo[x, 0];
 AppendTo[lam, 0];
 i++]
x = ReplacePart[x, 1 -> 10]; (* initial value assigned to x(0) *)
beta = 0.05;(* parameters *)
mu = 0.01;
gamma = 0.5;
P = 100;
w1 = 1;
While[test < 0, (*  while the tolerance is reached,repeat*)
    oldu = u;
    oldx = x;
    oldlam = lam;
    For[ i = 1, i < n, 
  k1 = beta*(P - x[[i]])*x[[i]] - (mu + gamma)*x[[i]] - u[[i]]*x[[i]];
  k2 = (beta*(P - x[[i]]) - 0.5*k1*h)*(x[[i]] + 0.5*k1*h) - (mu + 
       gamma)*(x[[i]] + 0.5*k1*h) - 
    0.5*(u[[i]] + u[[i + 1]])*(x[[i]] + 0.5*k1*h); 
  k3 = beta*(P - x[[i]] - 0.5*k2*h)*(x[[i]] + 0.5*k2*h) - (mu + 
       gamma)*(x[[i]] + 0.5*k2*h) - 
    0.5*(u[[i]] + u[[i + 1]])*(x[[i]] + 0.5*k2*h);
  k4 = beta*(P - x[[i]] - k3*h)*(x[[i]] + k3*h) - (mu + 
       gamma)*(x[[i]] + k3*h) - u[[i + 1]]*(x[[i]] + k3*h);
  ReplacePart[x, i + 1 -> x[[i]] + (h/6)*(k1 + 2*k2 + 2*k3 + k4)]; 
  i++ ];
 For[i = 1, i < n, j = n + 2 - i; 
  k1 = -w1 - 
    lam[[j]]*(beta*(P - x[[j]]) - beta*x[[j]] - (mu + gamma) - 
       u[[j]]); 
  k2 = -w1 - (lam[[j]] - 
       0.5*k1*h)*(beta*(P - x[[j]] + 0.5*k1*h) - (mu + gamma) - 
       0.5*(u[[j]] + u[[j - 1]])); 
  k3 = -w1 - (lam[[j]] - 
       0.5*k2*h)*(beta*(P - x[[j]] + 0.5*k2*h) - (mu + gamma) - 
       0.5*(u[[j]] + u[[j - 1]])); 
  k4 = -w1 - (lam[[j]] - 
       k3*h)*(beta*(P - x[[j]] + k3*h) - (mu + gamma) - u[[j - 1]]);
    ReplacePart[lam, 
   j - 1 -> lam[[j]] - (h/6)*(k1 + 2*k2 + 2*k3 + k4)]; i++];
 u1 = Min[100, Max[0, lam.x/2]];
 u = 0.5*(u1 + oldu);
 temp1 = Δ*Sum[Abs[u], {1, Length[u]}] - 
   Sum[Abs[oldu - u], {1, Length[u]}];
 temp2 = Δ*Sum[Abs[x], {1, Length[x]}] - 
   Sum[Abs[oldx - x], {1, Length[x]}];
 temp3 = Δ*Sum[Abs[lam], {1, Length[lam]}] - 
   Sum[Abs[oldlam - lam], {1, Length[lam]}];

 test = Min[temp1, Min[temp2, temp3]]; i++]
ListPlot[t, u]
ListPlot[t, x]

I'm getting error messages related to the indices, but I can't see what I did wrong.

Henrik Schumacher
  • 106,770
  • 7
  • 179
  • 309
Herr Schrödinger
  • 695
  • 3
  • 11
  • 2
    Some random things I noticed that are wrong: Clear[all] does not clear everything, it only clears all. For takes 4 arguments, you passed 3. To iterate from 1 to n, you'd use i <=n and not i < n in For. But I suggest you do not use For at all. Even for a procedural loop, start with Do. – Szabolcs Apr 05 '20 at 19:48
  • 1
    Don't use AppendTo. Do it like in the Matlab coe and initialize the vectors. E.g., initialize with x = ConstantArray[0.,n];x[[1]]=10.; Same for lam and u. That should solve already quite a lot of indexing problems. – Henrik Schumacher Apr 05 '20 at 19:50
  • 1
    Also, Sum[Abs[u], {1, Length[u]}] will return the vector Abs[u] Length[u]. You are probably looking for Total[Abs[u]]. – Henrik Schumacher Apr 05 '20 at 19:52
  • 1
    ReplacePart[lam, j - 1 -> lam[[j]] - (h/6)*(k1 + 2*k2 + 2*k3 + k4)] does nothing unless you write lam=ReplacePart[lam, j - 1 -> lam[[j]] - (h/6)*(k1 + 2*k2 + 2*k3 + k4)]. But that would be highly inefficient. Better use lam[[j - 1]] = lam[[j]] - (h/6)*(k1 + 2*k2 + 2*k3 + k4); – Henrik Schumacher Apr 05 '20 at 19:53
  • Moreover, I am pretty sure that many of the loops should better be replaced by vectorized operations. – Henrik Schumacher Apr 05 '20 at 19:56
  • 1
    @HenrikSchumacher Please, make an answer with the indicated corrections, I would like to accept it. – Herr Schrödinger Apr 05 '20 at 19:57

2 Answers2

8

According to chapter 9, "Mathematica’s NDSolve can take in boundary conditions, and system (9.26) can be directly input into it" (p. 239). Let's give it a try.

β = 0.05; μ = 0.01; γ = 0.5; n = 100; w1 = 1; i0 = 10; T = 0.9; umax = 100;

ust[t] := Min[umax, Max[0, λ[t] i[t]/2]];

sol = NDSolve[{
     i'[t] == β (n - i[t]) i[t] - (μ + γ) i[t] - ust[t] i[t],
     λ'[t] == -w1 - λ[t] (β (n - i[t]) - β i[t] - (μ + γ) - ust[t]),
     i[0] == i0, λ[T] == 0}, {i, λ}, {t, 0, T}][[1]];

Plot[Evaluate[ust[t] /. sol], {t, 0, T}, AxesLabel -> {"t", "u*"}]
Plot[Evaluate[i[t] /. sol], {t, 0, T}, AxesLabel -> {"t", "i"}]

enter image description here enter image description here

Chris K
  • 20,207
  • 3
  • 39
  • 74
5

I am not 100% sure whether this does the same as the the Matlab code, but this could be a start. Please double-check for correctness.

n = 100;
h = 1./n;
t = Subdivide[0., 1., n];
Δ = 0.001;
β = 0.05;
μ = 0.01;
γ = 0.5;
P = 100;
w1 = 1.;
forwardstep[x_, u_, u1_] := Module[{k1, k2, k3, k4},
   k1 = β (P - x) x - (μ + γ) x - u x;
   k2 = (β (P - x) - 0.5 k1 h) (x + 0.5 k1 h) - (μ + γ) (x + 0.5 k1 h) - 0.5 (u + u1) (x + 0.5 k1 h);
   k3 = β (P - x - 0.5 k2 h) (x + 0.5 k2 h) - (μ + γ) (x + 0.5 k2 h) - 0.5 (u + u1) (x + 0.5 k2 h);
   k4 = β (P - x - k3 h) (x + k3 h) - (μ + γ) (x + k3 h) - u1 (x + k3 h);
   x + (h/6.) (k1 + 2. k2 + 2. k3 + k4)
   ];
backwardstep[λ_, x_, u_, u1_] := Module[{k1, k2, k3, k4},
   k1 = -w1 - λ (β (P - x) - β x - (μ + γ) - u);
   k2 = -w1 - (λ - 0.5 k1 h) (β (P - x + 0.5 k1 h) - (μ + γ) - 0.5 (u + u1));
   k3 = -w1 - (λ - 0.5 k2 h) (β (P - x + 0.5 k2 h) - (μ + γ) - 0.5 (u + u1));
   k4 = -w1 - (λ - k3 h) (β (P - x + k3 h) - (μ + γ) - u1);
   λ - (h/6.) (k1 + 2. k2 + 2. k3 + k4)
   ];

u = ConstantArray[0., n + 1];
λ = ConstantArray[0., n + 1];
x = ConstantArray[0., n + 1];
x[[1]] = 10.;

test = -1.;
While[test < 0,
  oldu = u;
  oldx = x;
  oldλ = λ;
  Do[x[[i + 1]] = forwardstep[x[[i]], u[[i]], u[[i + 1]]], {i, 1, n}];
  Do[λ[[j - 1]] = backwardstep[λ[[j]], x[[j]], u[[j]], u[[j - 1]]], {j, -1, -n, -1}];
  u1 = Clip[0.5 λ x, {0., 100}];
  u = 0.5 (u1 + oldu);
  temp1 = Δ Total[Abs[u]] - Total[Abs[oldu - u]];
  temp2 = Δ Total[Abs[x]] - Total[Abs[oldx - x]];
  temp3 = Δ Total[Abs[λ]] - Total[Abs[oldλ - λ]];
  test = Min[temp1, Min[temp2, temp3]];
  ];
ListLinePlot[Transpose[{t, u}]]
ListLinePlot[Transpose[{t, x}]]
Henrik Schumacher
  • 106,770
  • 7
  • 179
  • 309