9

I am looking to solve the diffusion equation with a discontinuous jump in the diffusion coefficient. In 1D, the diffusion equation for $u(t,x)$ is: $$ \partial_t u = \partial_x (D \partial_x u), $$ where $D(x)$ is the spatially varying diffusion coefficient. Let's use $D(x) = 1$ if $x < 1$ and $D(x) = 3$ if $x > 1$.

Question: Is there a better/smarter way to handle the discontinuity than approximating the jump with a continuous function? Is there a way to solve the equation in a piecewise manner, on $x \in [0,1)$ with $D=1$, on $x \in (1,2]$ with $D=3$, and somehow impose the condition that $D^\text{left} \partial_x u^\text{left} = D^\text{right} \partial_x u^\text{right}$ at $x=1$?

What I am trying to avoid is the following approximation:

We can approximate the discontinuity in $D$ by a sharp continuous function.

diffConst[x_] := (1 + 2 LogisticSigmoid[50 (x - 1)])

Plot[diffConst[x], {x, 0, 2}, PlotRange -> {0, 3}]

enter image description here

Then we can solve the equation like so, with a sufficiently fine-grained spatial discretization:

fun = NDSolveValue[
  {
   D[z[x, t], t] == D[diffConst[x] D[z[x, t], x], x],
   z[0, t] == 2,
   z[2, t] == 1,
   z[x, 0] == 2
   },
  z,
  {x, 0, 2}, {t, 0, 20},
  Method -> {"PDEDiscretization" -> {"MethodOfLines", 
      "SpatialDiscretization" -> {"TensorProductGrid", 
        "MinPoints" -> 300}}}
 ]

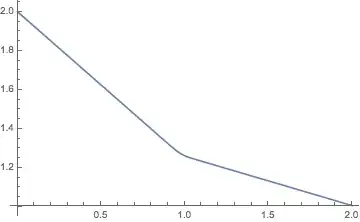
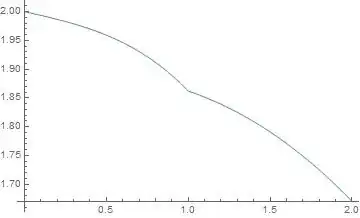
Plot the solution:

Animate[
 Plot[fun[x, t], {x, 0, 2}],
 {t, 0, 5}
]

enter image description here

user21
  • 39,710
  • 8
  • 110
  • 167
Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
  • In principle, FEM would not require any continuity of the diffusion constant (just make sure that there is a mesh node at the jump point). But I am not sure whether one can access this feature from the high-level user interface... – Henrik Schumacher Apr 07 '20 at 11:34
  • Follow-up question: https://mathematica.stackexchange.com/questions/218983/how-to-model-diffusion-through-a-membrane – Szabolcs Apr 07 '20 at 11:50
  • @Henrik Do you have any tips on the follow-up question I just linked? – Szabolcs Apr 07 '20 at 11:50
  • Well, I am afraid I would discretize both sides of the geometry separately, request the system matrices from the low-level FEM tools in Mathematica and couple the system by hand (with a hand-written time integrator). That would probably not help you. I recall that we had a discussion about similar couplings (just one dimension higher and for more general interfaces) in 193789. IIRC, @AlexTrounev understood pretty well how to set up things directly with NDSolve. – Henrik Schumacher Apr 07 '20 at 12:01
  • Related: https://mathematica.stackexchange.com/a/121739/1871 https://mathematica.stackexchange.com/q/131542/1871 – xzczd Apr 07 '20 at 12:29
  • 1
    Somehow I missed this: https://reference.wolfram.com/language/PDEModels/tutorial/PDEModelsOverview.html It almost certainly has comparable examples, but I will need some time to go through it. – Szabolcs Apr 07 '20 at 13:23
  • 1
    This is explained, for example, in the section Partial Differential Equations with Variable Coefficients – user21 Apr 08 '20 at 07:55

1 Answers1

11

Yes, it is possible to solve the equation in a piecewise manner : 

diffConst[x_]:=If[x<1,1,3];

fun = NDSolveValue[
  {
   D[z[x, t], t] == D[diffConst[x] D[z[x, t], x], x],
   z[0, t] == 2,
   z[2, t] == 1,
   z[x, 0] == 2
   },
  z,
  {x, 0, 2}, {t, 0, 20},
  Method -> {"PDEDiscretization" -> {"MethodOfLines", 
      "SpatialDiscretization" -> {"FiniteElement"(*, 
        "MinPoints" -> 300*)}}}
 ]
 Plot[{fun[x,0.4]},{x,0,2}]

enter image description here

Note that the function diffConst[x] D[z[x, t], x] is continuous : 

derivative = D[fun[x, .4], {x}]
Plot[{diffConst[x] derivative}, {x, 0, 2}]

enter image description here

This is very likely the solution you are expecting, because it corresponds to most physical situations. (For example, in thermics, It means conservation of the flux of heat thru the point x=1)

andre314
  • 18,474
  • 1
  • 36
  • 69