5

Does anyone know how could I plot the basis order functions for the following function (code below)?

An example of what I should expect is https://en.wikipedia.org/wiki/Lagrange_polynomial#/media/File:Lagrange_basis_functions.svg . Please note they use a different spatial grid, here xg

I am having difficulties deciding on how to plot each of the 7 basis functions. 

NN = 7 ; a = 0.0; b = 1.0 ;
xg = Table[(i (b - a))/NN, {i, 0, NN}];

Lagrg[X_, x_] :=
  Module[{j, k, n}, 
   n = Length[X] - 1; 
   For[ k = 0, k <= n, k++,
    L[n, k, x] = ( \!\(
\*UnderoverscriptBox[\(\[Product]\), \(j = 0\), \(k - 1\)]
\*FractionBox[\(x - 
\*SubscriptBox[\(X\), \(j\)]\), \(
\*SubscriptBox[\(X\), \(k\)] - 
\*SubscriptBox[\(X\), \(j\)]\)]\)) (\!\(
\*UnderoverscriptBox[\(\[Product]\), \(j = k + 1\), \(n\)]
\*FractionBox[\(x - 
\*SubscriptBox[\(X\), \(j\)]\), \(
\*SubscriptBox[\(X\), \(k\)] - 
\*SubscriptBox[\(X\), \(j\)]\)]\));  ]; 
   Return[  L[n, k, x] ]; ];

For clarity, also find the picture 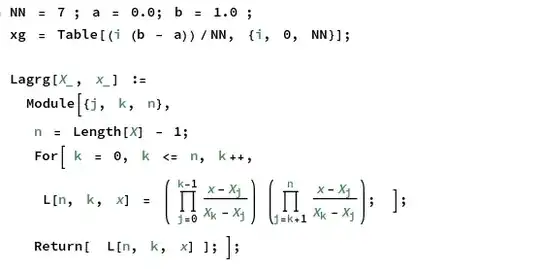CODE

Any ideas are welcomed. Thanks in advance.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
AriC
  • 97
  • 5
  • 1
    L[j_, xj_, x_] := Fold[Times, (x-#)/(xj[[i]]-#) &@Drop[xj, {i}]]. -- maybe? I'm on a phone and can't test. I can barely read what I've written. – Michael E2 Apr 08 '20 at 23:35
  • @MichaelE2, I have written it using mathematical objects, for clarity I am adding a picture. – AriC Apr 09 '20 at 07:53

2 Answers2

8

If you want to use Mathematica as it is designed to generate the Lagrange basis as a list of polynomials, then use InterpolatingPolynomial:

lBasis[nodes_, x_] := Table[
  InterpolatingPolynomial[
   Transpose@{nodes, UnitVector[Length@nodes, k]}, x],
  {k, Length@nodes}]

To plot them:

xj = {0, 2, 3, 7, 10, 11};
Plot[lBasis[xj, x] // Evaluate, {x, Min[xj], Max[xj]},
 Epilog -> {Red, Point@Thread[{xj, 1}], Point@Thread[{xj, 0}]},
 GridLines -> {xj, {1}}]

enter image description here

To get the same thing from my comment, fix the typo in the comment and use Table to list the basis:

L[i_, xj_, x_] := (* i-th Lagrange basis function *)
 Fold[Times, (x - #)/(xj[[i]] - #) &@Drop[xj, {i}]];
lBasis[nodes_, x_] := Table[L[k, nodes, x], {k, Length@nodes}]

If you want to write something like a C program as an exercise and not avoid the for loop, then maybe someone else can help with that.

Michael E2
  • 235,386
  • 17
  • 334
  • 747
1

Try this

Lagata2[Data_]:=Module[{XX=Data},
                ELI[XX_,i_]:=(X=Drop[XX,{i}];
                    Product[(x-X[[j,1]])/(XX[[i,1]]-X[[j,1]]), {j,1,Length[X]}]);
                Sum[XX[[i,2]]*ELI[XX,i],{i,1,Length[XX]}]
                    ]

To test it and compare with function. BTW, I use Labatto intervals

f[x_] = 1/(1+10x^4);
a=-5; b=5; n=24;
X = N[Table[(b+a)/2+(b-a)/2 Cos[(i*\[Pi])/n], {i, 0, n}]];
Y= f[X];
XY = Transpose[{X,Y}];
g[x_]=Lagata2[XY]//Expand

Plot[{g[x], f[x]}, {x,a,b},PlotRange->All, PlotLegends->"Expressions"]


''
Lucy Nowacki
  • 41
  • 3