function rep will take Derivative[0, 0, 1, 0][F][x, y, z, t] and
output diff[F[x,y,z,t],z]:
Just a quick hack, as I do not know of direct MMA command. Will let someone else come up with a one liner answer ;)
ClearAll[F, x, y, z, t];
rep[f_, g_] := Module[{h, vars = {}, n, i, deps = {}},
h = f[[0, 1]];
n = Length@f[[0, 0]];
Do[
If[(f[[0, 0]][[i]]) == 1, AppendTo[deps, f[[i]]]];
AppendTo[vars, f[[i]]]
, {i, 1, n}];
g[h[Sequence @@ vars], Sequence @@ deps]
]
Call as
rep[Derivative[0, 0, 0, 1][F][x, y, z, t], diff]
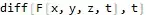
rep[Derivative[0, 0, 1, 1][F][x, y, z, t], diff]
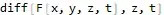
rep[Derivative[1, 0, 1, 0][F][x, y, z, t], diff]
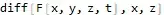
I am not sure how are you going to use this result, but this is what you asked for.
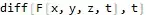
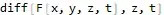
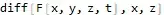
F^(0,0,1,0)[x,y,z,t]itself is not valid syntax. What is exactly the problem you are trying to solve? i.e. why do you need to do this in first place? – Nasser Apr 16 '20 at 20:26That's the plain text form of the output of D[F[x,y,z,t],z]On my version of Mathematica, this is the plain text ofD[F[x,y,z,t],z]I getInputForm[D[F[x, y, z, t], z]]givesDerivative[0, 0, 1, 0][F][x, y, z, t]so how did it come to beF^(0,0,1,0)[x,y,z,t]on your end? Since this is not valid mathematica syntax. It gives errorSyntax::sntxf: "(" cannot be followed by "0,0,1,0)".I am using V 12.1., which version of Mathematica are you using? – Nasser Apr 16 '20 at 20:32InputForm. That is what is read by Mathematica. Screen thing is just formatting for display purposes only. So your question should beHow to change Derivative[0, 0, 1, 0][F][x, y, z, t] to diff[F[x,y,z,t],z]that is all. (but what isdiff? Is this your own function? – Nasser Apr 16 '20 at 20:41D[F[x, y, z, t], z]is reallyDerivative[0, 0, 1, 0][F][x, y, z, t]. TryD[F[x, y, z, t], z]// InputFormto see. – Nasser Apr 16 '20 at 20:59