0

I have this (rather long) transcendental equation, that has multiple singularities where it goes to infinity, then reappears at negative infinity. When I try and find the roots of the equation via NSolve (or Reduce), it gives me the positions of the singularities as well as the zero crossings, which is incorrect:

enter image description here

However, when I look for a single root with FindRoot, it will only give me the position of a zero crossing, even if I give FindRoot a singularity as the search point. My question is - what command can I use to get the correct results I am getting from FindRoot, except for all roots within a certain domain, rather than one at a time? And my second question is, why are NSolve and Reduce giving me singularities as solutions when they are not solutions?

Here is my code - transcendental equation:

resonanceCondition = (1.0215026378769585`*^-7 Cos[
    0.038659981280734605` f] + 
  0.012261290032792185` Sqrt[f] Cos[0.038659981280734605` f] + 
  367.9364783156771` f Cos[0.038659981280734605` f] - 
  1.7385441873343195`*^-12 f^(3/2) Cos[0.038659981280734605` f] + 
  1.9168458821735513`*^11 f^2 Cos[0.038659981280734605` f] - 
  0.000905985363774135` f^(5/2) Cos[0.038659981280734605` f] - 
  27.186785669459642` f^3 Cos[0.038659981280734605` f] + 
  3.5778253945592175`*^-17 f^(7/2) Cos[0.038659981280734605` f] - 
  7.294985015701372`*^9 f^4 Cos[0.038659981280734605` f] + 
  1.349642838920257` f^(9/2) Cos[0.038659981280734605` f] + 
  0.0005593326523029028` f^5 Cos[0.038659981280734605` f] + 
  7.617136885646142`*^-25 f^(11/2) Cos[0.038659981280734605` f] + 
  145698.31404595848` f^6 Cos[0.038659981280734605` f] + 
  3.968314731945664`*^-16 f^(13/2) Cos[0.038659981280734605` f] + 
  1.190810871788677`*^-11 f^7 Cos[0.038659981280734605` f] + 
  0.003101895368576676` f^8 Cos[
    0.038659981280734605` f] + (1.0215026378769585`*^-7 + 
     0.012261290032792185` Sqrt[f] + 367.9364783156771` f + 
     1.73854418733432`*^-12 f^(3/2) + 
     1.916845882173552`*^11 f^2 + 
     0.0008919683885642353` f^(5/2) + 26.766164635165886` f^3 - 
     3.577825394559219`*^-17 f^(7/2) + 
     7.075853251101013`*^9 f^4 - 1.349642838920257` f^(9/2) - 
     0.0005593326523029029` f^5 - 
     7.617136885646143`*^-25 f^(11/2) - 145698.31404595854` f^6 - 
     3.968314731945666`*^-16 f^(13/2) - 
     1.190810871788677`*^-11 f^7 - 
     0.0031018953685766773` f^8) Cosh[
    2.8222`*^-11 + 1.6937701111797905`*^-6 Sqrt[f]] - 
  3.9263268389666276`*^-8 f Sin[0.038659981280734605` f] - 
  0.00471284462232609` f^(3/2) Sin[0.038659981280734605` f] - 
  141.42292112410644` f^2 Sin[0.038659981280734605` f] + 
  9.035967129830372`*^-7 f^(5/2) Sin[0.038659981280734605` f] - 
  7.422693884237215`*^10 f^3 Sin[0.038659981280734605` f] + 
  470.7485518941833` f^(7/2) Sin[0.038659981280734605` f] + 
  0.04187499717395471` f^4 Sin[0.038659981280734605` f] - 
  1.8614725761418453`*^-11 f^(9/2) Sin[0.038659981280734605` f] + 
  2.1815699347445037`*^7 f^5 Sin[0.038659981280734605` f] - 
  0.009697750162420625` f^(11/2) Sin[0.038659981280734605` f] + 
  8.2863`*^-10 f^6 Sin[0.038659981280734605` f] + 
  0.4316929951106164` f^7 Sin[
    0.038659981280734605` f] + (2.866240292375598`*^-17 + 
     5.160603931704003`*^-12 Sqrt[f] + 
     3.0971854210038807`*^-7 f + 0.006196017403536449` f^(3/2) + 
     53.38370833435124` f^2 + 3.203873913991683`*^6 f^(5/2) + 
     0.020624423363802637` f^3 - 
     1.8346263052726576`*^-6 f^(7/2) + 
     1.0744746292968111`*^7 f^4 - 955.7888618948019` f^(9/2) - 
     4.248775821083848`*^-7 f^5 - 
     3.6303916368586526`*^-14 f^(11/2) - 
     221.34930665701606` f^6 - 
     0.00001891332246165412` f^(13/2)) Sinh[
    2.8222`*^-11 + 
     1.6937701111797905`*^-6 Sqrt[
      f]])/(f (5.329080691237708`*^-19 + 
    6.396596693986087`*^-14 Sqrt[f] + 1.9194891031013206`*^-9 f + 
    1.` f^2) (-1.2730400062331583`*^9 Cos[
      0.038659981280734605` f] + 
    3.007633699724958`*^-6 Sqrt[f] Cos[0.038659981280734605` f] + 
    0.0902529952868547` f Cos[0.038659981280734605` f] + 
    4.7019279839115955`*^7 f^2 Cos[0.038659981280734605` f] + 
    6.396596693986088`*^-14 f^(5/2)
      Cos[0.038659981280734605` f] + 
    1.9194891031013215`*^-9 f^3 Cos[0.038659981280734605` f] + 
    1.` f^4 Cos[
      0.038659981280734605` f] + (-1.2730400062331583`*^9 - 
       3.007633699724958`*^-6 Sqrt[f] - 0.0902529952868547` f - 
       4.7019279839115955`*^7 f^2 - 
       6.396596693986088`*^-14 f^(5/2) - 
       1.9194891031013215`*^-9 f^3 - 
       1.0000000000000002` f^4) Cosh[
      2.8222`*^-11 + 1.6937701111797905`*^-6 Sqrt[f]] + 
    4.893155395016759`*^8 f Sin[0.038659981280734605` f] - 
    3.1263949972942227` f^(3/2)
      Sin[0.038659981280734605` f] + (-0.3572030481737306` - 
       21437.87990287647` Sqrt[f] - 71359.37236924547` f^2) Sinh[
      2.8222`*^-11 + 1.6937701111797905`*^-6 Sqrt[f]])) == 0;

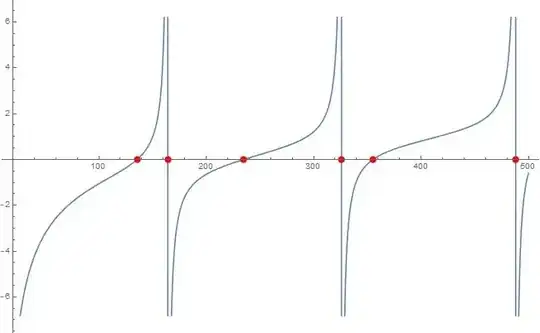
Finding and plotting the roots with NSolve:

sol = NSolve[(resonanceCondition ) && 20 < f < 500]
p1 = Plot[((resonanceCondition) // First) /. f -> freq, {freq, 20, 
    500}];
pts = Table[{f /. sol[[j]], (resonanceCondition // First) /. 
     sol[[j]]}, {j, 1, Length[sol]}]; 
p2 = ListPlot[pts, PlotStyle -> Red];
Show[p1, p2]

Comparing results with FindRoot:

FindRoot[(resonanceCondition // First) , {f, 165}]
FindRoot[(resonanceCondition // First) , {f, 164}]
Jeremiah Rose
  • 193
  • 5
  • 4
    Consider Plot[((resonanceCondition) // First) /. f -> freq, {freq, 164., 164.4}]. Note the range of your plot and this one. – Michael E2 Apr 18 '20 at 03:55
  • 1
    @MichaelE2 this means NSolve was correct, right? But OP said where it goes to infinity, then reappears at negative infinity. so I was wondering what is happening here. It looks OP then was wrong in this statement. – Nasser Apr 18 '20 at 04:03
  • 2
    @Nasser Yes, I believe NSolve is correct. The OP's plot shows the graph going to ±7, not to infinity actually. I think the OP misinterpreted the plot. – Michael E2 Apr 18 '20 at 04:06
  • Thanks for the insight @MichaelE2. Your comment has definitely opened up a whole can of worms in my understanding of what this physical system is doing. Do you know why FindRoot is not giving the positions of the "singularities", then? – Jeremiah Rose Apr 18 '20 at 04:28
  • 1
    @Jeremiah, since you're finding the roots of a ratio of two functions, have you considered just applying NSolve[]/FindRoot[] to the numerator only? – J. M.'s missing motivation Apr 18 '20 at 04:34
  • @J.M.'stechnicaldifficulties it turns out that NSolve's result was correct after all – Jeremiah Rose Apr 18 '20 at 04:35
  • 2
    Nevertheless, it would surely be less of a computational burden to just consider the numerator, unless you have good reason to believe that the numerator and denominator have common factors. – J. M.'s missing motivation Apr 18 '20 at 04:36
  • Update: turns out FindRoot[(resonanceCondition // First) , {f, 164.16}] actually does give me a root at f->164.163. – Jeremiah Rose Apr 18 '20 at 04:36
  • If you look at the plot in my first comment and keep in mind that to find f -> 164.163 by Newton's method the initial point has to be somewhat closer to the root than the local max and min nearby, it should help to understand FindRoot with the different starting points 164, 165, and 164.12. – Michael E2 Apr 18 '20 at 16:04

1 Answers1

2

This is just a long comment. Answer is given in comment above by @MichaelE2. The answer by NSolve is correct.

But if you want, you could always filter out solutions found, which are not as close to zero as you wanted as follows

sol = NSolve[resonanceCondition && 20 < f < 500]

Mathematica graphics

sel = If[Abs[ First[resonanceCondition]/. #] >10*$MachineEpsilon, False,True] & /@ sol;
sol = Pick[sol, sel]

Mathematica graphics

p1 = Plot[((resonanceCondition) // First) /. f -> freq, {freq, 20, 500}];
pts = Table[{f /. sol[[j]], (resonanceCondition // First) /. 
     sol[[j]]}, {j, 1, Length[sol]}];
p2 = ListPlot[pts, PlotStyle -> Red];
Show[p1, p2]

Mathematica graphics

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • 1
    Just to add: it is possible to use the MeshFunctions capability of Plot[] to find initial approximations for roots, which can then be passed to FindRoot[] for further polishing, cf. this thread. – J. M.'s missing motivation Apr 18 '20 at 04:25
  • @Nasser I was just using sol[[1;;;;2]] to filter results. Turns out that approach was VERY incorrect. – Jeremiah Rose Apr 18 '20 at 04:38
  • @JeremiahRose I would suggest filtering based on sensitivity: obj = resonanceCondition /. Equal -> Subtract; Abs[obj] < Abs[D[obj, f] * (f*$MachineEpsilon)] /. sol (accept a solution if True) where $\Delta f = $ f*$MachineEpsilon allows for an error in the last bit of the computed solution for f. Make $\Delta f$ larger if you want more tolerance. – Michael E2 Apr 18 '20 at 15:35