0

I'm new to Mathematica and really struggling with something seemingly simple. I'm trying to do an integration and keep the results in terms of the symbol $T_1$ and $A_i$:

$$ T_1=\frac{\text{pi} A_i}{2 J_a} $$

I want to integrate $j_1$:

$$ j_1=J_a \sin \left(\frac{\text{pi} t}{T_1}\right) $$

The result I get is:

$$ -\frac{1}{2} A_i \cos \left(\frac{2 t J_a}{A_i}\right) $$

I'm not sure how to get the results in terms of the desired variables. I understand that Mathematica evaluates symbols as early as possible, and so I have tried playing with Hold but it didn't help. I've also tried to recast the problem as simultaneous equations and then using Solve or Eliminate as mentioned here:

Rewriting expression in terms of factor

Here's an example of something I've tried:

$$ j_1=J_a \sin \left(\frac{\text{pi} t}{\text{Hold}\left[T_1\right]}\right) $$

$$ a_1 = Integrate[\%, t] $$

$$ \text{ReleaseHold}\left[\text{Solve}\left[\left\{\text{expr}=a_1,T_j=T_1\right\},\text{expr},\left\{J_a\right\}\right]\right] $$

I tried introducing $T_j$ since I figured $T_1=T_1$ probably wouldn't make sense.

The results are still in terms of $J_a$ though:

$$ \left\{\left\{\text{expr}\to -\frac{\text{pi} A_i^2 \cos \left(\frac{2 t J_a}{A_i}\right)}{4 J_a T_j}\right\}\right\} $$

Any advice greatly appreciated!

Dan Sandberg
  • 125
  • 5
  • It's also not a good idea to use anything with subscripts if you're, as you say, "new to Mathematica", since those are troublesome to use with anything except for pretty formatting. – J. M.'s missing motivation Apr 19 '20 at 12:00
  • Thanks, I didn't know. If I want to have constants t_1 through t_10 that are defined through other constants, and I want to be able to programmatically iterate through them, what is the suggested approach? An array format instead? t[[1]]? – Dan Sandberg Apr 19 '20 at 12:34
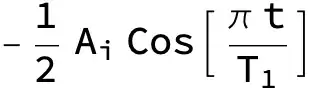
  • Yes, something like t[1] (that is, single brackets and not double ones) should work. – J. M.'s missing motivation Apr 19 '20 at 12:35
  • And what about for replacing letter subscripts, like A_j? Are dollar signed (A$j) used or what? Seems so ugly, guess I need to read about Symbolize and the Notation package.... – Dan Sandberg Apr 19 '20 at 12:37

1 Answers1

2
Format[Ai] := Subscript["A", "i"]
Format[T1] := Subscript["T", 1]

j1 = Ja Sin[π t/T1];

expr = Integrate[j1, t] /. Solve[T1 == π Ai/(2 Ja), Ja][[1]]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • Is there a way to do it where T1 is still defined? Because I need it (and T2, T3, ...) in other places. Didn't know about "Format", thanks! I could imagine using a Module or Block, but it seems so ugly... – Dan Sandberg Apr 19 '20 at 13:32
  • Define the replacement rule t1r = T1 -> π Ai/(2 Ja);

    Then whenever you want to replace T1 use expression /. t1r

     – Bob Hanlon Apr 19 '20 at 14:05
  • Perhaps I'm misunderstanding, but if I only have the replacement rule then there would be no way for the system to know there is a relationship between T1 and Ja and so I'd either have answers without T1 (if I used the replacement rules) or I'd have answers with a mix of T1 and Ai/Ja, but without the simplifications that can result by knowing how they inter-relate. – Dan Sandberg Apr 19 '20 at 14:24
  • If you Set the value of T1, i.e. T1 = ... then T1 can never appear since it will always be replaced by its definition. A rule enables you to either not use the rule and let T1 appear or use the rule and thereby substitute for T1. Alternatively, you can define the equation T1 == ... and use the equation in a system of equations (Solve, Eliminate, Reduce, FindInstance, ...) or as an assumption in Simplify or similar. – Bob Hanlon Apr 19 '20 at 14:37
  • Ok, that makes sense, thank you! If I want to do the system of equations route, do I need to do something like eq1 = T1 == ..., eq2 = T2 == ..., or is there some way to reference the T1 == and T2 == without assigning the equality to another symbol? – Dan Sandberg Apr 19 '20 at 19:32
  • Just include the equations in a list: eqns = {T1 == def1, T2 == def2, ...} – Bob Hanlon Apr 19 '20 at 19:38
  • Using a system of equations created all sorts of issues for me so I ended up going with your first suggestion. Thanks! – Dan Sandberg Apr 21 '20 at 14:24