I would like to plot a segment of a circular annulus in three dimensions with constant thickness (like a thick washer, but through some limited ranges of angle). This shows the shape:
RegionPlot3D[
(5 < Sqrt[x^2 + y^2] < 6 && 5 < z < 6 && 0 < ArcTan[x, y] < .5) ,
{x, -10, 10}, {y, -10, 10}, {z, -10, 10},
Mesh -> None,
PlotPoints -> 100,
PlotStyle -> Directive[Opacity[0.5], Red]]
However, this requires an extremely high number of PlotPoints (which will be undesirable in my full figure, containing many dozens of such shapes). Moreover I would like to retain the thin edge lines and impose Opacity[], colors, and so forth, as can be applied in all Graphics3D primitives such as Cylinder[].
I could work with Regions, such as this start:
Region[
RegionDifference[Cylinder[{{0, 0, 0}, {0, 0, 1}}, 1],
Cylinder[{{0, 0, 0}, {0, 0, 1}}, 1/2]]]
but here too I won't get the thin edge lines and opportunity to adjust the overall opacity and color as I seek.
In two dimensions, there is a perfect graphics element:
Graphics[{Opacity[0.5], Orange, Annulus[{0, 0}, {1/2, 1}, {0, .3}]}]
What I'm seeking would be called Annulus3D. In the absence of such a 3D primitive, how shall I plot what I seek?
Just to show the final result (using the linked code from @kglr, below):





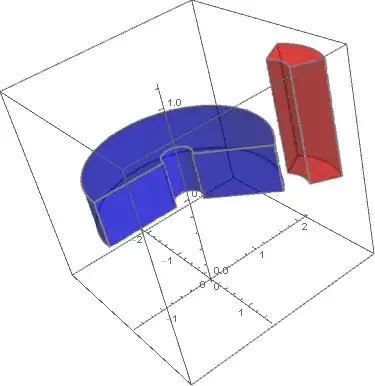
Graphics3D[{Opacity[0.5],EdgeForm[Blue],Red,Cylinder[]}]on my region wedge? – David G. Stork Apr 21 '20 at 00:23