I've got an interpolation function:
iFunction =
Interpolation[{{0, 0}, {2.*^-6, 6.642*^-11}, {4.*^-6,
2.9691*^-10}, {6.*^-6, 7.0932*^-10}, {8.*^-6,
1.3125*^-9}, {0.00001, 2.1122*^-9}, {0.00003,
2.1497*^-8}, {0.00005, 6.2317*^-8}, {0.00007,
1.2489*^-7}, {0.00009, 2.0924*^-7},
{0.0002, 1.0561*^-6}, {0.0004, 4.1822*^-6}, {0.0006,
9.2208*^-6}, {0.0008, 0.000016043}, {0.001, 0.000024544}, {0.003,
0.00018695}, {0.005, 0.00046129}, {0.007, 0.00082275}, {0.009,
0.001256}, {0.02, 0.0045473}, {0.04, 0.012822}, {0.06, 0.022605},
{0.08, 0.033154}, {0.1, 0.044102}, {0.3, 0.15245}, {0.5,
0.24488}, {0.7, 0.32188}, {0.9, 0.38668}, {1.1, 0.44191}, {1.3,
0.48952}, {1.5, 0.53096}, {1.7, 0.56735}, {1.9, 0.59953}, {2.1,
0.62818}, {2.3, 0.65382}, {2.5, 0.67688}, {2.7, 0.69772},
{2.9, 0.71663}, {3.1, 0.73385}, {3.3, 0.74958}, {3.5,
0.76399}, {3.7, 0.77724}, {3.9, 0.78944}, {4.1, 0.80071}, {4.3,
0.81114}, {4.5, 0.82081}, {4.7, 0.8298}, {4.9, 0.83817}, {6.,
0.87532}, {8., 0.91793}, {10., 0.94308}, {12., 0.95899}}]
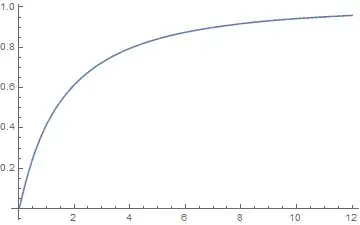
At first glance, it appears to be doing what I want it to do:
Plot[iFunction[r], {r, 0, 12}]
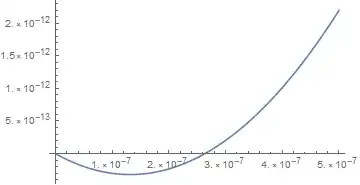
But when I use this function as part of a FindMinimum operation, I'm getting negative values (which are not part of the valid domain). Upon further inspection, I find that if I zoom in on the function towards zero, I get this:
Plot[iFunction[r], {r, 0, 5*10^-7}]
Clearly, this was never my intent but the FindMinimum still considers this to be part of the solution space. I understand that this function is fitting the data with a polynomial function, but is there a way of telling the Interpolation function that negative numbers are not part of the domain?