Drawing an arc inside an angle

Question

Assuming we have two lines which define an angle

a10 = Graphics[{Line[{{5.9, -0.3}, {7.1, 1.3}}]}];
a11 = Graphics[{Arrowheads[0.025], Thick, Arrow[{{5.9, -0.3}, {5.9, 1.95}}]}]; 
plot = Show[{a10, a11}]

How can we draw a vector arc for identifying the angle? It would be nice to be able to control the size of the arc and also its relative position (how low or high from the center of the angle).

You can draw arc using Circle[{x,y},…,{θ1,θ2}] gives a circular or ellipse arc from angle θ1 to θ2. — vi pa, Apr 23 '20 at 09:05
@vipa I don't want just a part of circle but an arc with a vector. — Vaggelis_Z, Apr 23 '20 at 09:09
You can use, as you have already done Arrow[curve,…] to represents an arrow following the specified curve. — vi pa, Apr 23 '20 at 09:14
The solution here combined with Arrow[] should suit your needs. — J. M.'s missing motivation, Apr 23 '20 at 09:44
I'm sorry but seem that Arrow don't work with Circle as curve. — vi pa, Apr 23 '20 at 11:00
Related: https://mathematica.stackexchange.com/q/197995/1871 — xzczd, Apr 25 '20 at 02:06

vi pa · Accepted Answer · 2023-04-22T18:36:17.470

I have create this function:

angleArc[vCenter_, startPoint_, endPoint_,radius_]:=Module[{c=vCenter,p1=endPoint,p2=startPoint},
ang[center_,p_]:=If[center[[1]] < p[[1]] && center[[2]] < p[[2]], ArcTan[(p[[2]] - center[[2]])/(p[[1]]-center[[1]])],
If[center[[1]] > p[[1]] &&(center[[2]] <= p[[2]] || center[[2]] > p[[2]]), Pi + ArcTan[(p[[2]] - center[[2]])/(p[[1]] - center[[1]])],
If[center[[1]] < p[[1]] && center[[2]] < p[[2]], 2Pi + ArcTan[(p[[2]]-center[[2]])/(p[[1]] - center[[1]])],
If[center[[1]] == p[[1]] && center[[2]] < p[[2]], Pi/2, 3Pi/2]]]];
{Circle[c,radius,{ang[c,p1],ang[c,p2]}],
If[ang[c,p1] < ang[c,p2],
Arrow[{{radius Cos[ang[c,p1] + 0.01], radius Sin[ang[c,p1] + 0.01]} + c,
{radius Cos[ang[c,p1]], radius Sin[ang[c,p1]]} + c}], 
Arrow[{{radius Cos[ang[c,p1] - 0.01], radius Sin[ang[c,p1] - 0.01]} + c,
{radius Cos[ang[c,p1]], radius Sin[ang[c,p1]]} + c}]]}]

where vCenter is the coordinate of the vertex of the angle, startPoint is any coordinate of a point on the start side of the angle, endPoint is any coordinate of a point on the end side of the angle, and radius is the radius of the arc.

Counterclockwise arc:

Graphics[{Line[{{5.9, -0.3}, {7.1, 1.3}}],Line[{{5.9, -0.3}, {5.9, 1.95}}],
angleArc[{5.9, -0.3},{7.1, 1.3},{5.9, 1.95},1]}]

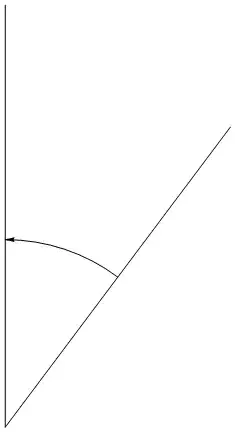
Clockwise arc:

Graphics[{Line[{{5.9, -0.3}, {7.1, 1.3}}],Line[{{5.9, -0.3}, {5.9, 1.95}}],
angleArc[{5.9, -0.3},{5.9, 1.95},{7.1, 1.3},1]}]

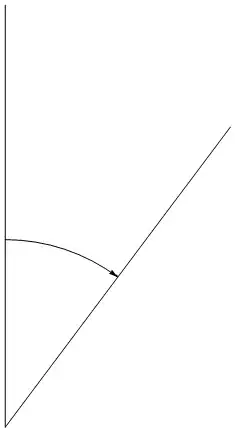
Edit

As indicated by @Cesareo in the comment below in the previous code there in same little bug. The correct one should be:

angleArc[vCenter_, startPoint_, endPoint_,radius_]:=Module[{c=vCenter,p1=endPoint,p2=startPoint},
ang[center_,p_]:=Which[
center[[1]] < p[[1]] && center[[2]] < p[[2]],
 ArcTan[(p[[2]] - center[[2]])/(p[[1]]-center[[1]])],
center[[1]] > p[[1]] &&(center[[2]] <= p[[2]] || center[[2]] > p[[2]]),
    Pi + ArcTan[(p[[2]] - center[[2]])/(p[[1]] - center[[1]])],
center[[1]] < p[[1]] && center[[2]] >= p[[2]],
    2Pi + ArcTan[(p[[2]]-center[[2]])/(p[[1]] - center[[1]])],
center[[1]] == p[[1]] && center[[2]] < p[[2]],
    Pi/2, 
    True, 3Pi/2];
{Circle[c,radius,{ang[c,p1],ang[c,p2]}],
If[ang[c,p1] < ang[c,p2],
Arrow[{{radius Cos[ang[c,p1] + 0.01], radius Sin[ang[c,p1] + 0.01]} + c,
{radius Cos[ang[c,p1]], radius Sin[ang[c,p1]]} + c}], 
Arrow[{{radius Cos[ang[c,p1] - 0.01], radius Sin[ang[c,p1] - 0.01]} + c,
{radius Cos[ang[c,p1]], radius Sin[ang[c,p1]]} + c}]]}]

Now the code work for the example in the comment:

Graphics[{Line[{{0, 0}, {7.1, 0}}], Line[{{0, 0}, {7.1, -4.}}], angleArc[{0, 0}, {7.1, 0}, {7.1, -4.}, 1]}]

Needs correction. Try for instance Graphics[{Line[{{0, 0}, {7.1, 0}}], Line[{{0, 0}, {7.1, -4.}}], angleArc[{0, 0}, {7.1, 0}, {7.1, -4.}, 1]}] — Cesareo, Apr 20 '23 at 11:43

score 3 · Answer 2 · edited Apr 25 '20 at 01:50

I suggest you use the GraphicsTools package from Terry Honan. The zipped package files are available here.

<< GraphicsTools`

The example from his notebooks:

With[{W = 50}, 
 Graphics[{Arrowheads[.1], With[{θ = Angle[{6, 4}, {1, 0}]},
           Rotate[{{CoordinateAxes[{-48, 53}, {-25, 40}, ArrowSize -> 3],
           Text["⊥", {53, -5}], 
           Text["∥", {-5, 40}],
          {AbsoluteDashing[3], 
           Line[{W {-Cos[θ], 0}, 
           W {-Cos[θ], Sin[θ]}, W {0, Sin[θ]}}]},
           AngleLabel[{180 ° - θ, 180 °}, 15, 23, "θ"],
            AbsoluteThickness[2],
          {Red, LabeledArrow[W {Cos[θ], 0}, Style["N", Italic], 
           TextOffset -> -.6]},
           LabeledArrow[ {30, 5}, {30, 5 + 25}, Style["a",Italic], TextOffset ->-.6],
         {Brown, 
           LabeledArrow[{-3.5, 0}, {-3.5, 0} + .8 W {0, Sin[θ]}, 
           "\!\(\*SubscriptBox[\(f\), \(k\)]\)", TextOffset -> .8, 
          TextPosition -> .7]},
         {Blue, 
          LabeledArrow[W {-Cos[θ], Sin[θ]}, 
          Style["m g", Italic], TextOffset -> {2.9, -.6}],  
          LabeledSegment[W {0, Sin[θ]}, 
          Style["m g sinθ", Italic], TextOffset -> {.5, -1.}],          
          LabeledSegment[W {-Cos[θ], 0}, 
          Style["m g cosθ", Italic], 
          TextOffset -> 1.6]}}}, θ + 90 °, {0, 0}] /. 
          t_Text :> Rotate[t, -θ - 90 °]]
         }, BaseStyle -> {12, FontFamily -> "Times"}, 
         PlotRange -> {{-50, 50}, {-60, 50}}]]

All credits should go to Terry Honan.

Drawing an arc inside an angle

2 Answers2