Is there any way to force Mathematica to write 1 + Cot[a] + Tan[a] in
form or Sec[a] and Csc[a]? That would eliminate Cot[a] and Tan[a]
Yes, if this is what you meant.
ClearAll[a];
Simplify[TrigReduce[Tan[a]/(1 - Cot[a]) + Cot[a]/(1 - Tan[a])]]
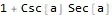
The only other way to do in general is like this
ClearAll[a, x];
expr = Tan[a]/(1 - Cot[a]) + Cot[a]/(1 - Tan[a]);
expr /. {Tan[x__] :> HoldForm@(Sin[x]/Cos[x]), Cot[x__] :> HoldForm@(Cos[x]/Sin[x])}

This should work for any expression. But note that if you want to do anything with that expression, then you need to release the hold at that moment. Using ReleaseHold[...].
As I mentioned in comment, I do not know how this can be done in general. There might be a way to do it using special transformation rules passed to Simplify, since Simplify in general uses LeafCount to simply expressions.
I tried TransformationFunctions but could not make it work. I think this is because Mathematica will write Sin[x]/Cos[x] back to Tan[x] immediately. I am out of my bag of ticks.
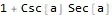

Tan[a]=x, then the final expression is1+1/x+x. What do you mean by get rid ofxin this? Only whenx=Iorx=-IwhereIissqrt(-1)will you get rid ofx. ButTan[x]can never be complex. – Nasser Apr 24 '20 at 04:561 + Cot[a] + Tan[a]in form orSec[a] and Csc[a]? That would eliminateCot[a]andTan[a]. – Real Noob Apr 24 '20 at 04:59