How do I keep the Standard Form from reducing negative powers?

Question

I have the following input form:

R[η_] := (3*Subscript[ρ, B]*aEta[η]^-3)/(4*Subscript[ρ, γ]*aEta[η]^-4)

It's supposed to look like this: $$R[\eta\_]:=\frac{3 \rho_B\space a_{\eta}[\eta]^{-3}}{4\space\rho_{\gamma}\space a_{\eta}[\eta]^{-4}}$$ But when I convert it to Normal Form, Mathematica attempts to simplify the negative powers and I get: $$R[\eta\_]:= \frac{3\rho_B}{\frac{a_{\eta}[\eta]^3(4\rho_{\gamma})}{a_{\eta}[\eta]^4}}$$ Is there anyway to force the Standard Form to show the way it's supposed to look (i.e. the way the formula is traditionally written in the textbooks). Perhaps some association operator that can't be overridden when converting from Input to Standard?

What exactly do you want to work? Are you trying to print the definition, are you calling StandardForm in an input cell, ... typically you would use a HoldForm, Inactivate, or Matex for this — user5601, Apr 30 '20 at 00:09
This is an input cell. I've gotten in the habit of hitting Ctrl+Alt+I in order to see the raw form, then Ctrl+Alt+N to have Mathematica do the typesetting. I want the first equation to show up when I switch to Standard Form, but I'm getting the second equation. — Quark Soup, Apr 30 '20 at 00:47
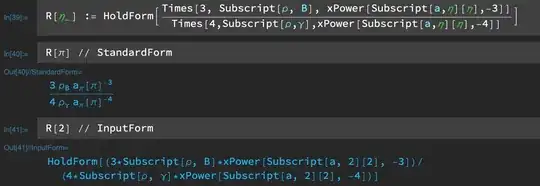
Please add all your code needed to reproduce this, e.g. you haven’t defined aEta — user5601, Apr 30 '20 at 00:53
You basically want one Power typeset in StandardForm and the other two Power left alone. Examine carefully Hold[ R[\[Eta]_] := (3*Subscript[\[Rho], B]*aEta[\[Eta]]^-3)/(4* Subscript[\[Rho], \[Gamma]]*aEta[\[Eta]]^-4) ] // FullForm and note the form of the RHS is num * Power[den, -1]. I'd try entering the definition using control-/. — Michael E2, Apr 30 '20 at 01:05

score 2 · Accepted Answer · edited May 05 '20 at 21:41

Sometimes I forget the fact that

FullForm[x^-2] === FullForm[1/x^2] (* True *)

Borrowing a trick from another post, perhaps this will work for you:

xPower /: MakeBoxes[xPower[x_, e_ /; e < 0], form_] := SuperscriptBox[MakeBoxes[x, form], MakeBoxes[e, form]] 
xPower := Power 
R[\[Eta]_] := HoldForm[Times[3, Subscript[\[Rho], B], xPower[Subscript[a,\[Eta]][\[Eta]],-3]]/Times[4,Subscript[\[Rho],\[Gamma]],xPower[Subscript[a,\[Eta]][\[Eta]],-4]]]
R[\[Pi]] // StandardForm

I can't think of a solution that will let you keep using those shortcuts mentioned in the comments. Sometimes you just have to separate the display of a symbol from its function.

Also, on macOS, the shortcuts for converting a selection to StandardForm or InputForm is Command + Shift + N and Command + Shift + I respectively.

How do I keep the Standard Form from reducing negative powers?

1 Answers1