Represent a Concave Mesh Volume

Question

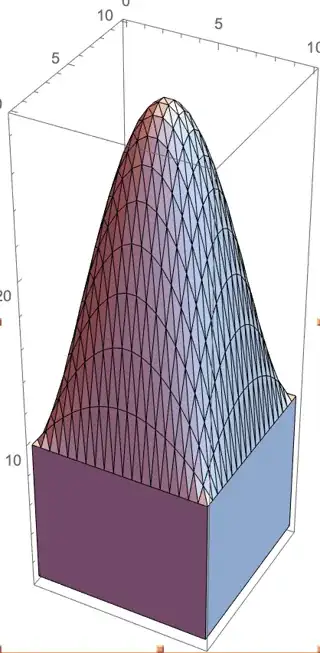
I programmatically generate a shape, where the top surface is defined by a series of polygons. I generate all the points of the polygon.

polygonCoord = 
  N[ToExpression[
     Import["https://pastebin.com/raw/1TqJ9xRs", "List"]][[1]]];

poly = Polygon[polygonCoord];

(*this looks great*)
Graphics3D[poly, Axes -> True]

(*and I can create a Mesh object, with Region Dimension 3, no problem*)


DelaunayMesh[Flatten[polygonCoord, 1]]

Graphics 3D and the Mesh object look great:

For a concave shape, it doesn't work

polygonCoord = 
  N[ToExpression[
     Import["https://pastebin.com/raw/TH3yTHH7", "List"]][[1]]];

poly = Polygon[polygonCoord];

(* this looks great *) 
Graphics3D[poly, Axes -> True]

(* but I have no way to create a Mesh, from which I can use useful \
functions like RegionDistance[] and RegionNearest[] in Region \
Dimension 3 *) 

DelaunayMesh[Flatten[polygonCoord, 1]]
ConvexHullMesh[Flatten[polygonCoord, 1]]

Graphics 3D looks good:

But the Mesh Object doesn't work:

Any ideas how I can use the polygon coordinate data to create the shape I want?

Maybe this can help: (86277), (38178). Include also the word "alpha-shape" to your list of search keywords. — Henrik Schumacher, May 07 '20 at 12:46

score 4 · Accepted Answer · answered May 07 '20 at 15:42

Since both DelaunayMesh and ConvexHullMesh work on convex shapes, you probably should not expect them to work on concave shapes. You could split out the first 5 coordinate groups representing the base and do a difference operation with the rest of the points.

polygonCoord = 
  N[ToExpression[
     Import["https://pastebin.com/raw/JYeSyxyp", "List"]][[1]]];
regbase = DelaunayMesh[Union@Flatten[polygonCoord[[1 ;; 5]], 1]];
regshape = DelaunayMesh[Union@Flatten[polygonCoord[[6 ;; -1]], 1]];
regdiff = RegionDifference[regbase, regshape]

Represent a Concave Mesh Volume

1 Answers1