2D and 3D graphics that project a world map on Icosahedron

Question

I would like to generate 2D and 3D graphics of icosahedron with continuous world map projected on them. An example is provided as follows:

It's trivial to generate 3D Icosahedron using GraphicsComplex. We can add texture. However, I am not sure how to add the continuous texture on it. Anyone has suggestions? Many thanks!

Vitaliy Kaurov · Answer 1 · 2020-05-10T03:54:42.960

Slightly changed last example from docs on GeoProjection. There are a few issues, for instance textures have different resolution. If I figure things out I'lll update the answer. But I thought this is a good start for you anyway.

PolyhedronProjection[polyhedron_]:=
Module[{pts3D,center,pts2D,proj,pts2Dprojected,geographics,plotrange,pts2Dscaled,rescale},
rescale[{x_,y_},{xs_,ys_}]:={Rescale[x,xs],Rescale[y,ys]};
Graphics3D[{
pts3D=First[#];
center=Mean[pts3D];
center=GeoPosition[GeoPositionXYZ[center,Norm[center]]];
pts2D=GeoPosition[GeoPositionXYZ[pts3D,Norm[pts3D[[1]]]]];
proj={"Gnomonic","Centering"->center};
pts2Dprojected=Most/@GeoGridPosition[pts2D,proj][[1]];
geographics=GeoGraphics[{Opacity[0],center,GeoPath[pts2D[[1]],
    CurveClosed->True]},GeoProjection->proj,GeoZoomLevel->1,
    GeoBackground->"CountryBorders"];
plotrange=PlotRange/.AbsoluteOptions[geographics,PlotRange];
pts2Dscaled=rescale[#,plotrange]&/@pts2Dprojected;
{Texture[ImageData[Rasterize[geographics[[1]],"Image"]]],
Polygon[pts3D,VertexTextureCoordinates->pts2Dscaled]}}&/@
N@Flatten[PolyhedronData[polyhedron,"Faces","Polygon"]],
Boxed->False,SphericalRegion->True]]


PolyhedronProjection["Icosahedron"]

score 6 · Answer 2 · answered May 10 '20 at 04:01

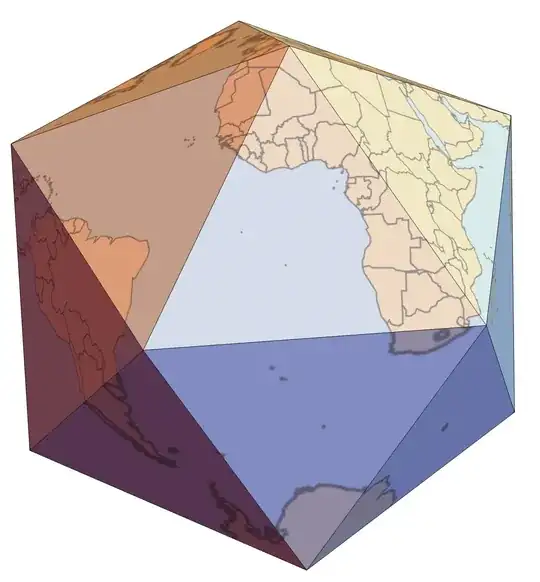
~ 6 years ago, I wrote a little routine for gnomonically projecting a spherical texture onto a polyhedron:

(* Newell's algorithm for face normals *)
newellNormals[pts_List?MatrixQ] := With[{tp = Transpose[pts]}, 
      Normalize[MapThread[Dot, {ListConvolve[{{-1, 1}}, tp, {{2, -1}, {2, -1}}], 
                                ListConvolve[{{1, 1}}, tp, {{-2, -1}, {-2, -1}}]}]]]

(* https://mathematica.stackexchange.com/a/167114 *)
    vectorRotate[vv1_?VectorQ, vv2_?VectorQ] := 
     Module[{v1 = Normalize[vv1], v2 = Normalize[vv2], c, d, d1, d2, t1, t2},
            d = v1.v2;
            If[TrueQ[Chop[1 + d] == 0],
               c = UnitVector[3, First[Ordering[Abs[v1], 1]]];
               t1 = c - v1; t2 = c - v2; d1 = t1.t1; d2 = t2.t2;
               IdentityMatrix[3] - 2 (Outer[Times, t2, t2]/d2 - 
               2 t2.t1 Outer[Times, t2, t1]/(d2 d1) + Outer[Times, t1, t1]/d1),
               c = Cross[v1, v2];
               d IdentityMatrix[3] + Outer[Times, c, c]/(1 + d) - LeviCivitaTensor[3].c]]

Options[polyhedronProjection] = {Padding -> 1., Resampling -> Automatic};
polyhedronProjection[Polygon[pts_?MatrixQ], img_Image, opts : OptionsPattern[]] := 
    Module[{eps = 0.05, h, ptp, tex, trf, tri},
           tri = AffineTransform[{vectorRotate[{0, 0, 1}, newellNormals[pts]], 
                                  Mean[pts]}];
           trf = InverseFunction[tri];
           ptp = Drop[trf /@ pts, None, -1]; h = Max[Abs[ptp]];
           tex = ImageTransformation[img, 
                                     If[Graphics`PolygonUtils`InPolygonQ[(1 + eps) ptp, #], 
                                        Function[{x, y, z},
                                                 {Arg[x + I y], ArcSin[z] + π/2}] @@ 
                                        Normalize[tri[Append[#, 0.]]], -{4, 1}] &, 
                                     AspectRatio -> Automatic,
                                     DataRange -> {{-π, π}, {0, π}},
                                     PlotRange -> {{-h, h}, {-h, h}}, 
                                     Sequence @@ FilterRules[{opts} ~Join~
                                                          Options[polyhedronProjection], 
                                                          Options[ImageTransformation]]];
           {Texture[tex],
            Polygon[pts, VertexTextureCoordinates -> Rescale[ptp, {-h, h}]]}]

Using, for instance, the ETOPO1 global relief,

etopo1 = Import["http://www.ngdc.noaa.gov/mgg/image/color_etopo1_ice_low.jpg"];

we can do the following:

ico = First @ Normal[MapAt[ScalingTransform[{1, 1, 1}/
                                            PolyhedronData["Icosahedron", "Circumradius"]], 
                           N[PolyhedronData["Icosahedron", "GraphicsComplex"]], 1]];

Graphics3D[{EdgeForm[], polyhedronProjection[#, etopo1] & /@ ico}, 
           Boxed -> False, Lighting -> "Neutral"]

icosahedral world

The method works for any polyhedron that can be inscribed in a unit sphere. For example, one of my previous Gravatars was based on "TruncatedIcosahedron":

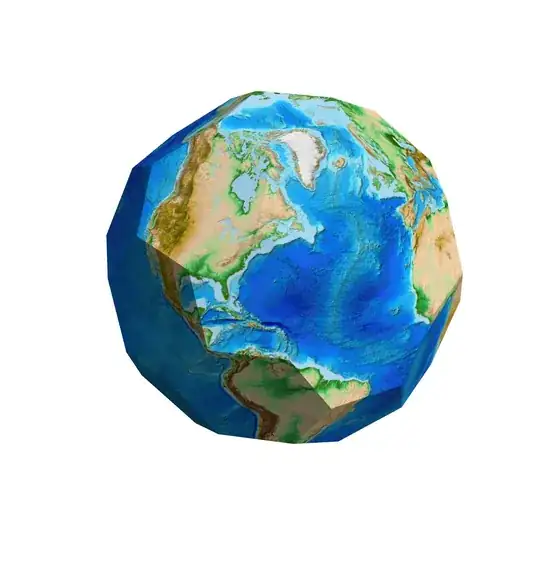
Buckyworld

See this reference as well.

However, I have not been successful in modifying this method so that it can be used on the result of PolyhedronData["Icosahedron", "Net"]; I'd be interested in seeing someone else do so.

Additionally, there are other possible projections of a sphere onto a polyhedron. Snyder devised an equal-area map projection, while Lee gives a conformal projection onto the dodecahedron, which can be mapped onto an icosahedron as well by virtue of duality. I'll leave all those for someone else to do.

2D and 3D graphics that project a world map on Icosahedron

2 Answers2