FEM 2D mesh with inclusion

Question

I want to create a FEM mesh with an inclusion, but I want to define the coordinates of the edge nodes manually, since I need the nodes for a problem that requires periodic boundary conditions.

The definition of the geometry is not the problem, but I do not know how to incorporate the coordinated of the edge nodes into the mesh.

Is there a possibility to do it with mathematica?

Thanks in advances.

Max

Answer 1

Mathematica does not require a one-to-one nodal correspondence for the PeriodicBoundaryCondition to work. However, care must be taken to ensure that PeriodicBoundaryCondition does not share nodes with a DirichletCondition.

Here is an example adapted for an inclusion taken from the documentation for PeriodicBoundaryCondition. Please note that there can be artefacts introduced due to implied NeumannConditions on the "source" boundary as discussed in this MSE post. That is why I applied forward and reverse PBC's. It seemed to work.

Needs["NDSolve`FEM`"]
{length, height, xc, yc, r} = {1, 2, 0, 0, 1/8};
{sx, sy, fx, fy} = {-length/2, -height/2, length/2, height/2};
disk = Region@Disk[{xc, yc}, r];
Ω = 
  RegionDifference[Rectangle[{sx, sy}, {fx, fy}], disk];
mesh = ToElementMesh[Ω, MaxCellMeasure -> 0.0005, 
   AccuracyGoal -> 5];
pde = ((Inactive[
       Div][(-{{1, 0}, {0, 1}}.Inactive[Grad][u[x, y], {x, y}]), {x, 
       y}]) - If[1/4 fx <= x <= 3/4 fx && sy/4 <= y <= fy/4, 1., 
     0.] == 0)
Subscript[Γ, D] = 
  DirichletCondition[
   u[x, y] == 0, (y <= sy || y >= fy) && sx < x <= fx];
pbcf = PeriodicBoundaryCondition[u[x, y], x == sx && sy <= y <= fy, 
   TranslationTransform[{length, 0}]];
pbcr = PeriodicBoundaryCondition[u[x, y], x == fx && sy <= y <= fy, 
   TranslationTransform[{-length, 0}]];
ufun = NDSolveValue[{pde, pbcf, pbcr, Subscript[Γ, D]}, 
   u, {x, y} ∈ mesh];
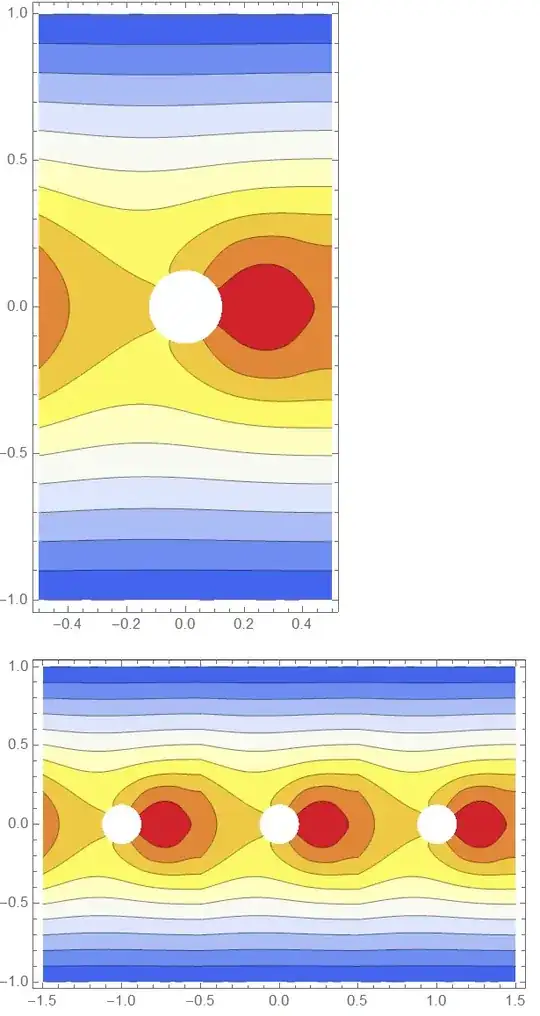
cp = ContourPlot[ufun[x, y], {x, y} ∈ mesh, 
  ColorFunction -> "TemperatureMap", AspectRatio -> Automatic]
Show[MapAt[Translate[#, {length, 0}] &, cp, 1], cp, 
 MapAt[Translate[#, {-length, 0}] &, cp, 1], PlotRange -> All]

For completeness, I show the artefact with specifying only one PBC resulting in a no flux condition on the source wall.

pbc = PeriodicBoundaryCondition[u[x, y], x == sx && sy <= y <= fy, 
   TranslationTransform[{length, 0}]];
ufun = NDSolveValue[{pde, pbc, Subscript[Γ, D]}, 
   u, {x, y} ∈ mesh];
cp = ContourPlot[ufun[x, y], {x, y} ∈ mesh, 
  ColorFunction -> "TemperatureMap", AspectRatio -> Automatic]
Show[MapAt[Translate[#, {length, 0}] &, cp, 1], cp, 
 MapAt[Translate[#, {-length, 0}] &, cp, 1], PlotRange -> All]

Answer 2

I'm not sure if I'm misunderstanding your question, but it sounds like all you want is to control the positions of the nodes at the boundary.

<<NDSolve`FEM`
lpts = Cases[
  Table[{x, y}, {x, -10, 10}, {y, -10, 10}], 
  {a_, b_}/;Abs[a] == 10 || Abs[b] == 10,
  2
];
hexpts = CirclePoints[4, 6];
bmesh = ToBoundaryMesh[
  "Coordinates" -> Join[lpts, hexpts],
  "BoundaryElements" -> {
    LineElement[Partition[Last@FindShortestTour[lpts], 2, 1, {1, 1}]],
    LineElement[Partition[Range[6], 2, 1, {1, 1}] + Length[lpts]]
  },
  "RegionHoles" -> {{0, 0}}
];
mesh = ToElementMesh[bmesh];
Show[
  mesh["Wireframe"],
  Graphics[{
    Red,
    Point@lpts
  }]
]

I'm importing the FEM tools from NDSolve as I find they allow more control over mesh creation. I'm generating a matrix of regularly spaced points and then using Cases to select only the boundary points and saving them as lpts. These will be unordered for now. Then I generate the points necessary for the hexagon as hexpts.

ToBoundaryMesh wants a list of all the coordinates under the "Coordinates" argument, so I join lpts and hexpts. Then I add some "BoundaryElements". The first LineElement is the square outer edge. I'm using FindShortestTour to find the ordering that gives me a square and then partitioning this ordering to give me a list of consecutive point numbers like {{1, 2}, {2, 3},...,{n - 1, n}, {n, 1}}. This part wants just the position in the "Coordinates" list and not the actual coordinates themselves. Then I do the same thing for the hexagonal points which will be at the very end of the list, so I add the length of lpts to all of those positions. The last step of creating the boundary mesh is to specify that the hexagon at the centre should be a hole.

I generate a full mesh from this boundary mesh. You should be able to pass this mesh directly to NDSolve as you might any other type of mesh. Finally, I'm displaying the mesh along with the lpts I generated originally to make sure they match the edge nodes. You should be able to customize the lpts to be whatever you like. I tried generating a few different lpts and they always seemed to match the nodes.