I suspect you must have used a different function when you found an acceptable fit with Python.
Here is your data OCR'd from your previous question:
data = {{6.806883, -4.95593692818423 Exp[-41]}, {6.813879, 0.2966197}, {6.81548, 0.2090413},
{6.815993, 0.1047412}, {6.816116, 0.2172217}, {6.816141, 0.0175237}, {6.816558, 0.0401401},
{6.820772, 0.1076685}, {6.831049, 0.273381182476389}, {6.832778, 0.0872403214012297},
{6.835968, 0.213306278687343}, {6.837872, 0.196895932533893}, {6.839626, 0.182350945974245},
{6.842643, 0.236392340715514}, {6.843521, 0.385921906058286}, {6.843593, 0.44360591444177},
{6.845431, 0.395308588265182}, {6.848036, 0.347737788675773}, {6.85891, 1.2787088},
{6.861215, 1.6855233}, {6.87505, 2.5303902}, {6.888942, 3.59352405445488},
{6.893837, 3.64575756470423}, {6.895161, 3.68408863938315}, {6.89668, 3.66514216133916},
{6.897294, 3.67968886871024}, {6.903002, 3.70207215134901}, {6.908976, 3.67924971763244},
{6.911722, 3.72623544133449}, {6.914223, 3.74474620992355}, {6.917128, 3.75346349648285},
{6.927654, 3.79135369927254}, {6.930277, 3.76666521763759}, {6.93606, 3.8084950461229},
{6.9368, 3.66412103183458}, {6.948534, 3.9201313112154}, {6.949261, 3.81452649019695},
{6.956995, 3.84714584756615}, {6.959176, 3.83848603610872}, {6.968645, 3.85332287228747},
{6.971786, 3.85285653238902}, {6.972535, 3.8534977067291}, {6.981893, 3.86037751083982},
{6.98856, 3.8623598856111}, {6.997314, 3.87119143404958}, {7.013482, 3.88232714899738},
{7.018697, 3.87935255435361}, {7.033174, 3.88806880842605}, {7.058705, 3.89906031937574},
{7.061641, 3.90162364008693}, {7.066072, 3.90278794110276}, {7.080686, 3.9021178571306},
{7.088082, 3.90925888041691}, {7.089749, 3.90931704384336},
{6.795619, -1.74834441633166 Exp[-41]}};
ListPlot[data]

Running
f[T_?NumericQ] := NIntegrate[y^5/((1 - Exp[-y]) (Exp[y] - 1)), {y, 0, (d/T)}]
FindFit[data, (T^5/d^4) f[T], {{d, 0.01}}, T]
does result in the error you mention (and one other error you didn't mention).
Because there is only a single parameter to fit we can find a value of $d$ that minimizes the root mean square error:
rmse[d_] := Sqrt[(1/(Length[data] - 1)) Total[
Table[(data[[i, 2]] - (data[[i, 1]]^5/d^4) NIntegrate[y^5/((1 - Exp[-y]) (Exp[y] - 1)),
{y, 0, (d/data[[i, 1]])}])^2, {i, Length[data]}]]]
A plot of rmse over values of d:
Plot[rmse[d], {d, 0.01, 20}]

What does the fitted function look like with $d=0.01$ ?
Show[ListPlot[data],
Plot[(t^5/0.01^4) NIntegrate[y^5/((1 - Exp[-y]) (Exp[y] - 1)), {y, 0, (0.01/t)}], {t, 6.8, 7.1}]]
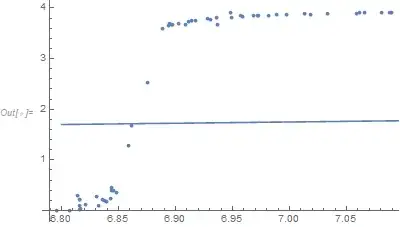



(T^5/d^4) f[T]over the range of your data for various values ofd. I think you'll find that the proposed function is inadequate to summarize your data. – JimB May 14 '20 at 16:48dthat python provided for the fit? – Bob Hanlon May 14 '20 at 18:57