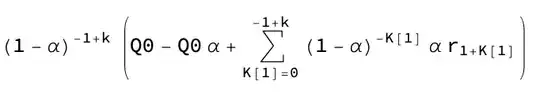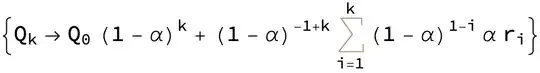Using RSolve for recurrence equation

Question

I'd like to use Mathematica to verify the solution to a recurrence equation. I have the following equation:

$Q_{k+1} = Q_k + \alpha(r_{k+1} - Q_k)$.

I also have a derivation showing how to obtain a solution for any $k$:

$Q_k = Q_{k-1} + \alpha(r_k - Q_{-1})$

$\ \ \ \ = \alpha r_k + (1 - \alpha)Q_{k-1}$

$\ \ \ \ = \alpha r_k + (1 - \alpha)\alpha r_{k-1} + (1 - \alpha)^2Q_{k-2}$

$\ \ \ \ = (1 - \alpha)^kQ_0 + \sum_{i=1}^k\alpha (1 - \alpha)^{k-i}r_i$,

where $Q_0$ is some arbitrary constant. However, when I use RSolve, I get a different answer.

RSolve[Q[k] == Q[k - 1] + \[Alpha] (Subscript[r, k] - Q[k - 1]), Q[k], k]

gives me the solution:

$(1 - \alpha)^{k-1}\mathbb{c}_1+(1-\alpha)^{-1+k}\sum_{K[1]=0}^{-1+k}(1-\alpha)^{-K[1]}\alpha r_{1+K[1]}.$

This is close but not exactly what I want. So what am I missing here?

Suba Thomas · Accepted Answer · 2020-05-14T19:51:34.867

7

You are missing the initial condition Q[0] == Q0.

Q[k] /. RSolve[{Q[k] == Q[k - 1] + α (Subscript[r, k] - Q[k - 1]), Q[0] == Q0}, 
    Q[k], k][[1]] // FullSimplify

This is equivalent to

$$(1-\alpha )^k Q0+\sum _{K[1]=1}^k \alpha\ (1-\alpha )^{k-K[1]}\ r_{K[1]}$$

edited May 14 '20 at 19:51

answered May 14 '20 at 19:44

Suba Thomas

8,716
1
17
32

Great that works. I thought the $\mathbb{c}_1$ constant was the value for the initial condition, but I guess not. Do you know where it comes from if it's not the value for Q[0]? – whaaswijk May 14 '20 at 20:54
@whaaswijk I do not know that. – Suba Thomas May 14 '20 at 21:15

score 5 · Answer 2 · answered May 14 '20 at 20:30

5

Clear["Global`*"]

Format[Q[k_]] := Subscript[Q, k];
Format[Q0] = Subscript[Q, 0];

Include the initial condition in RSolve

sol = (RSolve[
      {Q[k] == Q[k - 1] + \[Alpha] (Subscript[r, k] - Q[k - 1]), Q[0] == Q0},
      Q[k], k][[1]] // Simplify) /. K[1] -> i

Translate the index of summation

sol2 = ((sol /. Sum -> Inactive[Sum]) /.
    Inactive[Sum][expr_, {i, imin_, imax_}] :>
     Inactive[Sum][(expr /. i -> i - 1), {i, imin + 1, imax + 1}]) //
  Collect[#, Q0] &

Simplify the summation term

(sol3 = sol2 /. (expr1_ * Inactive[Sum][expr2_, {i, imin_, imax_}]) :> 
     Inactive[Sum][expr1*expr2, {i, imin, imax}]) // Activate

answered May 14 '20 at 20:30

Bob Hanlon

157,611
7
77
198

This is very nice, but it's using some advanced Mathematica magic that I'm not familiar with. I had no idea that you could do things like translating the index of summation. I'll have to look at the documentation to see exactly how this all works. – whaaswijk May 14 '20 at 20:58
1

That was some deft use of Inactive and Collect. – Suba Thomas May 14 '20 at 21:09

Using RSolve for recurrence equation

2 Answers2