0

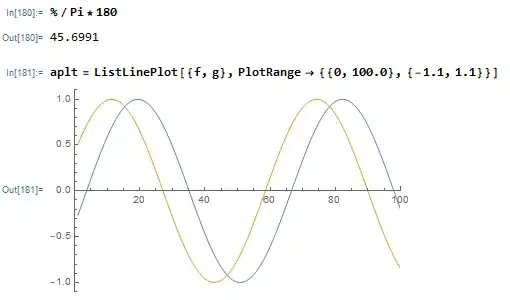
I would like to calculate the phase between two signals like 

f= Table[Sin[x-0.8],{x,-100,100,0.1}]
g= Table[Sin[x],{x,-100,100,0.1}]

For doing that I use the ArcCos[Correlation[f, g]], that instruction gives the phase between two functions but is independent of the sign of the phase. There is some way to consider the sign of the phase?

Thanks

F.Mark
  • 599
  • 2
  • 8
  • No, they use the same function. – F.Mark May 31 '20 at 13:56
  • 1
    @F.Mark I don’t understand what you mean. The question linked by Marius seems to fit your problem exactly! Can you explain why that solution would not work here? – MarcoB May 31 '20 at 16:09

1 Answers1

1

A phase of 45.6991 degrees? Followed Mariusz's advice, the graph shows different. (19? degrees)

f = Table[Sin[x - 0.8], {x, -100, 100, 0.1}];
g = Table[Sin[x], {x, -100, 100, 0.1}];

ffts1B = Fourier[f, FourierParameters -> {-1, 1}];
ffts2B = Fourier[g, FourierParameters -> {-1, 1}];
maxB = Max[Abs[ffts1B]];
posB = First[First[Position[Abs[ffts1B], maxB]]];
Arg[ffts1B[[posB]]] - Arg[ffts2B[[posB]]]

%/Pi*180
(* Out 45.6991 *)
aplt = ListLinePlot[{f, g}, PlotRange -> {{0, 100.0}, {-1.1, 1.1}}]

graphic of plot from original data

Seeing your Trig.

Sin[x-0.8] - Sin[x-0.0]
In:= 0.2*Pi/2/Pi*180
(* Out= 18. *)

My guess at the answer? 18 degrees.

prog9910
  • 630
  • 4
  • 10