4

I was messing around in Mathematica and I ended up trying this out:

GraphPlot3D[GraphData[{"MengerSponge", 3}]]

which produced the following (you can see a video here: https://youtu.be/FDvTEcHdBDs):

enter image description here

I don't really understand what I'm looking at. What does each vertex represent? What does each edge represent? What does the location of each vertex in 3D space represent?

I'm just really failing to see the relationship between this and a Menger Sponge.

Vitaliy Kaurov
  • 73,078
  • 9
  • 204
  • 355
EllipticalInitial
  • 1,111
  • 8
  • 13

1 Answers1

7

"The nth-order Menger Sponge graph is the connectivity graph of cubes in the nth iteration of the Menger sponge fractal." ~ mathworld. So cubes are the vertices, and the neighboring cubes get an edge between them. You do not recognize Menger Sponge because Graph is applying some built-in GraphLayout, most probably "SpringElectricalEmbedding". So instead of grid-like layout, you see what would happen to the cubes of Menger Sponge if they were electrically charged points connected by springs so that they minimize mechanical and electrical energy (or some other standard optimizing layout).

To see this very simply look at low iterations. Here how Menger Sponge looks for iteration 1:

men = MengerMesh[1, 3]

enter image description here

If you try a graph of those cubes connectivity you will not get a Menger Sponge -like looking thing due to a different graph layout:

Graph3D[GraphData[{"MengerSponge", 1}]]

enter image description here

But with proper vertex coordinates you can rearrange this layout to look exactly similar to the original Menger fractal:

Graph3D[GraphData[{"MengerSponge",1}],
VertexCoordinates->(Mean[MeshCoordinates[men][[#]]]&/@MeshCells[men,3][[All,1]])]

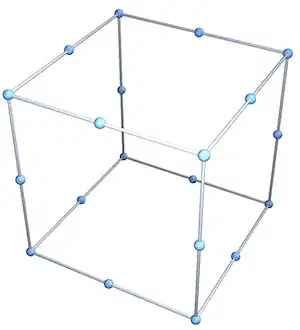
enter image description here

And in the same way the 3rd iteration can be rearranged too:

men=MengerMesh[3,3];
GraphPlot3D[GraphData[{"MengerSponge",3}],PerformanceGoal->"Speed",
VertexCoordinates->(Mean[MeshCoordinates[men][[#]]]&/@MeshCells[men,3][[All,1]])]

enter image description here

Vitaliy Kaurov
  • 73,078
  • 9
  • 204
  • 355
  • Thank you, this was very helpful, but is there any way to verify that it is indeed using the "SpringElectricalEmbedding" graph layout, as you suggest? If so, how? – EllipticalInitial Jun 01 '20 at 19:48
  • @jippyjoe4 You can simply put that object you got inside Graph[object, GraphLayout -> "SpringElectricalEmbedding"] to se if it gives the same layout. You can also try all other layouts mentioned in docs. – Vitaliy Kaurov Jun 01 '20 at 19:51
  • Thank you. I tried a few and it seems like I get the result in my original picture if I use "GravityEmbedding". SpringElectricalEmbedding gives me this: https://i.imgur.com/ECDPvu4.png – EllipticalInitial Jun 01 '20 at 20:15