2

There is a figure given that shows the relation between Forward current(y axis) and forward Voltage (x axis ) for a forward biased diode, with the given formula

$$If(forward current)= I0*e^{(k*q*T*Vf)/n}$$

Where $n=2, q=1.6*10^-19 , k=1.3805*10^-23$, Vf is the forward voltage and i am guessing T is the temperature.

The data points are given for If and for Vf. I need to use ListPlot to model the data as a function and then plot the characteristic curve for the silicon diode.

I don’t know what steps i need to provide (or what program i need to construct) in order to be able to plot a perfect curve for the diode so that when i try to insert the data points on the plotted curve they fit or are close.

I used Interpolation to function the data points firstly and then i used list plot command to plot the data points list. Then when i used plot command to plot the points given to find the curve, it keeps giving error! How do i proceed?

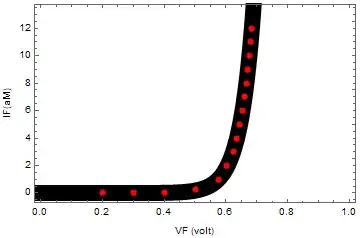
IF = {0.0, 0.0, 0.02, 0.25, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9, 10, 11, 12, 13}
VF = {0.2, 0.3, 0.4, 0.5, 0.576, 0.603, 0.624, 0.636, 0.646, 0.654, 0.661, 0.667, 0.671, 0.676, 0.681, 0.684}
Riffle[VF, IF]
data = Partition[%, 2]

f1 = Interpolation[data]

PLOT1 = ListPlot[f1, Joined -> False, PlotRange -> {{0.0, 1.0}, {0, 13}}, PlotStyle -> {Red}, PlotMarkers -> {Style["\[CircleDot]", Red, Smaller]}, Frame -> True, FrameLabel -> {"VF (volt)", "IF(aM)"}, LabelStyle -> Directive[Black]]

CurveThickness = 0.05

PLOT2 = Plot[f1[VF], {VF, 0.0, 1.0}, PlotRange -> All, Frame -> True, 
FrameLabel -> {"VF (volt)", "IF (aM)"}, 
LabelStyle -> Directive[Black], 
PlotStyle -> {Black, Thickness[CurveThickness]}]
MarcoB
  • 67,153
  • 18
  • 91
  • 189
Hannah_Zak
  • 129
  • 4
  • 3
    Please show us the code you have tried. – John Doty Jun 03 '20 at 11:45
  • how do i show that on here using mathematica? – Hannah_Zak Jun 03 '20 at 12:51
  • @JohnDoty is the code i entered correct? i am just trying to plot the characteristic curve for the diode at given data points. i tried using Fit Command but the formula/ equation i was required to enter didnt have enough information. – Hannah_Zak Jun 03 '20 at 13:21
  • I think the idea of the problem might be for you to fit the points to the model given by the formula you posted. Look into NonlinearModelFit. Then you can plot your raw data with ListPlot, the fit you found with Plot, and combine the two together using Show. – MarcoB Jun 03 '20 at 14:11
  • @MarcoB can u just show me how? i tried using the nlmf command letting the forward voltage be the variable but it didnt give any curve. – Hannah_Zak Jun 03 '20 at 14:32

1 Answers1

1

You have an extra value of IF for the number of values of VF you had, so I am commenting out the last one in your data. Also, rather than Riffle and Partition, I'd obtain the same thing with Transpose.

IF = {0., 0., 0.02, 0.25, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12(*, 13*)};
VF = {0.2, 0.3, 0.4, 0.5, 0.576, 0.603, 0.624, 0.636, 0.646, 
      0.654, 0.661, 0.667, 0.671, 0.676, 0.681, 0.684};
data = Transpose[{VF, IF}];

(* given parameter values *)
CurveThickness = 0.05
n = 2;
q = 1.6*^-19;
k = 1.3805*^-23;

(* Carry out the non-linear fit of data to your model *)
nlmf = NonlinearModelFit[data, i0 Exp[k q T Vf/n], {i0, T}, Vf];

(* generate and combine the two plots               *)
(* note that shared options have been moved to Show *) 
(* rather than duplicating them in both plots       *)
Show[
  (* plotting the results of the fit *)
  Plot[
    nlmf[Vf], {Vf, 0, 1}, 
    PlotStyle -> Directive[Black, Thickness[CurveThickness]]
  ],
  (* plotting the raw data *)
  ListPlot[
    data, 
    PlotStyle -> Directive[PointSize[0.02], Red], 
    LabelStyle -> Directive[Black]
  ],
  PlotRange -> {{0.0, 1.0}, {0, 13}},
  Frame -> True,
  LabelStyle -> Directive[Black], 
  FrameLabel -> {"VF (volt)", "IF(aM)"}
]

plot

MarcoB
  • 67,153
  • 18
  • 91
  • 189
  • its a perfect fit! wow that rarely happens in practicals. btw whats the difference if i had used Interpolation instead of NonLinearModelFit? why not use Fit only ? – Hannah_Zak Jun 03 '20 at 16:14
  • @Haneen Interpolation and fitting are conceptually different: an interpolation always goes through the points you feed it, by definition: that's what it's supposed to do! A fit will find the best parameter values in a given model to get as close as possible to your data, but typically may not go through them exactly. I wonder if this is "synthetic" data, i.e. made up by whoever wrote the problem, or really experimental values. – MarcoB Jun 03 '20 at 16:29
  • @Haneen Finally, Fit would have given the same results, but NonlinearModelFit is the more modern version that given you access to an easier to use solution and to statistics on the fit "for free". See this for further details: Difference between Fitting Algorithms. – MarcoB Jun 03 '20 at 16:30
  • oh thank you so much, your definitions cleared out everything. – Hannah_Zak Jun 03 '20 at 17:42