I do not agree that this is a bug in Mathematica. Mathematica has built-ins with certain optimizations. It is well done and a competitive CAS.
The solution from Bob Hanlon seems to be too difficult for the other engaging themself in answering this question.
So be aware that:
Reduce[{f[x, y] == 0, g[x, y] == 0}, {x, y}]
C[1] \[Element]
Integers && ((x == (2 I \[Pi] C[1])/Log[2] &&
y == 2) || (x == (I (4 \[Pi] C[1] + 19 I Log[2]))/(2 Log[2]) &&
y == 19/2) || (x == (
100 I \[Pi] + 200 I \[Pi] C[1] - 575 Log[2] +
17 Sqrt[561] Log[2] -
100 (Log[2] + Log[5] - Log[17 + Sqrt[561]]))/(100 Log[2]) &&
y == 1/100 (575 - 17 Sqrt[561])))
By that solution, the parameter C[1] is getting a cleared meaning.
$Version
"12.0.0 for Mac OS X x86 (64-bit) (April 7, 2019)"

The mathematical problem is rather difficult. I saw an example of how modern CAS calculates the representation of a polynomial function in 1D. It is at most a reciprocal refinement. The same is done with Solve or Reduce.
The algorithm for themself relies on strategy sometimes explicit, sometimes implicit. There is a need for a covering strategy and not for just fast finding solutions.
In this very case of 2-dimensional functions, there are in general points as solutions or curves as solutions possible. That is not in general taken into account using Solve or Reduce.
Select[Solve[{f[x, y] == 0, g[x, y] == 0}, {x, y}] /. C[1] -> 0,
FreeQ[#, Complex] &]
(* {{x -> 0, y -> 2}, {x -> -(19/2), y -> 19/2}} *)
The C[1] is such a strategic selection of methods.
Make before selecting methods for solutions, in general, an easy graphical consideration for example for selected regions. The might be conducted in the form of a general curve discussion and setting up and proving inequalities of equalities.
This example class has
ContourPlot[f[x, y] - g[x, y] == 0, {x, -5, 5}, {y, 0, 4}]

This curve of infinitely many solutions has the

This curve is rather complicated:

around the jump in the first ContourPlot. This is natural for such classes of implicit functions.
Excuse that there is no better representation of the arising chaos in the region
{{0,2.85},{1.495,1.53}}. There two cases:
(a) zoom into a done plot and get Zick zack and single points
(b) restrict to the named region and continue calculating more and more points. In this case, the curve starts to an extent in a spike towards lower x.
Despite the desire for a real-valued solution this problem has to be solved in the complexes giving it four instead of two dimensions for all solutions. So my opinion.
The problem type is already mentioned in the Mathematica documentation for ContourPlot. In the chapter Possible issues there are two examples for the problems related to zero crossings. The second example states, "Contours f(x,y)==0 for functions where f(x,y)>=0 are always poorly detected: " and shows:
f1[x_?NumberQ, y_?NumberQ] := Boole[x^2 + y^2 <= 1]
ContourPlot[f[x, y] == 0, {x, -1, 1}, {y, -1, 1}]
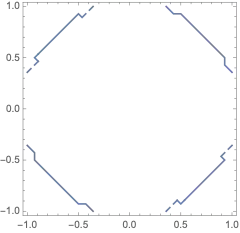 .
.
This is a foundational mathematical problem in pure generality. Respect for Mathematics and Numerics Experts at all not only at Wolfram Inc..
To dig deeper, my suggestion is to search math literature on the topics of zero-crossings!


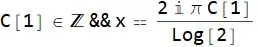







Solve[{f[x, y] == 0 , g[x, y] == 0}, {x, y}, Integers]by changingRealstoIntegers– flinty Jun 08 '20 at 13:57C[1] -> 0. Indeed, it seems that Something goes wrong when asking for real solutions. – MarcoB Jun 08 '20 at 14:02