Solution given by DSolve is correct, it just can't be verified by naive substitution.
This problem is similar to, but a bit more involved than your previous one. First of all, as done in my previous answer, we introduce a positive $\epsilon$ to the solution:
eq = D[u[x, t], t] - k D[u[x, t], x, x] == 0;
ic = u[x, 0] == 0;
bc = u[0, t] == p[t];
sol =
u[x, t] /.
First@DSolve[{eq, ic, bc}, u[x, t], {x, t},
Assumptions -> k > 0 && x > 0 && t > 0]
solfuncmid[x_, t_] =
Inactivate[
sol /. h_[a__, Assumptions -> _] :> h[a] /. {K[2], 0, t} -> {K[2],
0, t - ϵ} // Evaluate, Integrate]
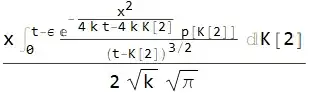
Remark
The rule h_[a__, Assumptions -> _] :> h[a] removes the Assumptions option to make the solution look good and avoid unnecessary trouble in subsequent verification, the Inactivate[…] is
necessary for v12.0.1 to make subsequent calculation faster, because the Integrate in output of DSolve in v12.0.1 isn't wrapped by Inactive.
Substitute it back to the PDE and combine the integrals:
residual = eq[[1]] /. u -> solfuncmid // Simplify
residual2 = With[{int = Inactive@Integrate}, residual //.
HoldPattern[coef1_. int[expr1_, rest_] + coef2_. int[expr2_, rest_]] :>
int[coef1 expr1 + coef2 expr2, rest]] // Simplify // Activate

Remark
The . in coef1_. is the shorthand for Optional, it's added so
the following type of pattern matching will happen:
aaa /. coef_. aaa -> (coef + 1) b
(* 2 b *)
Just the same as in the previous answer, when $\epsilon \to 0$ the … Exp[-(…)^2] can be replaced with a … DiracDelta[…]:
residual3 = residual2 /. Exp[coef_ a_^2] :> DiracDelta[a]/Sqrt[-coef] Sqrt[Pi]
(* (x DiracDelta[x] p[t - ϵ])/(Sqrt[k] Sqrt[1/(k ϵ)] ϵ^(3/2)) *)
Given that $x>0$, DiracDelta[x] == 0, so we've verified the solution satisfies the PDE.
Remark
Though Simplify can be used in last step to show residual3 == 0, I've avoided it
because of the issue mentioned
here.
Verification of initial condition (i.c.) is trivial:
solfuncmid[x, t] /. {t -> 0, ϵ -> 0} // Activate
What's really new compared with the previous problem is the verification of boundary condition (b.c.). The solution only satisfies the b.c. when $x \to 0^+$, so a direct substitution won't work, and doesn't make sense actually, because generally the integral in sol diverges at $x=0$. (Notice Integrate[1/(t - s)^(3/2), {s, 0, t}] diverges. )
Remark
One can also turn to numeric calculation to convince oneself. Here's a quick test with $p(t)=t$:
With[{int = Inactive[Integrate]},
solfuncmid[x, t] /.
coef_ int[a__] :> int[a] /. {k -> 1, ϵ -> 0, t -> 2,
Integrate -> NIntegrate, x -> 0, p -> Identity}] // Activate
(* NIntegrate::ncvb *)
(* 2.6163*10^33 *)
To verify the b.c., we transform the solution based on integration by parts:
soltransformed =
With[{int = Inactive[Integrate]},
Assuming[{t > K[2], k > 0, x > 0, t > 0, ϵ > 0},
solfuncmid[x, t] /.
int[expr_ p[v_], rest_] :>
With[{i = Integrate[expr, K[2]]},
Subtract @@ (i p[K[2]] /. {{K[2] -> t - ϵ}, {K[2] -> 0}}) -
int[i p'[K[2]], rest]] // Simplify] //.
coef_ int[a_, b__] :> int[coef a, b]]

Then we take the limit $\epsilon \to 0^+$. It's a pity Limit can't handle soltransformed all at once (this is reasonable of course, the unknown function p[t] is on the way), but by calculating
Limit[Gamma[1/2, x^2/(4 k ϵ)], ϵ -> 0,
Direction -> "FromAbove", Assumptions -> {k > 0, x > 0}]
(* 0 *)
separately, we know the correct limit (assuming p[t] is nice enough) is
sollimit = soltransformed /. x^2/(4 k ϵ) -> Infinity /. ϵ -> 0

Now we can substitute $x=0$:
sollimit /. x -> 0 // Activate // Simplify

Integrate refuses the calculate further, which is again reasonable, but it's clear the expression above simplifies to p[t] assuming p[t] is a nice enough function, so the b.c. is verified.
Tested on v12.0.1, v12.1.0.
Just for fun, here's a solution based on Fourier sine transform:
Clear@fst
fst[(h : List | Plus | Equal)[a__], t_, w_] := fst[#, t, w] & /@ h[a]
fst[a_ b_, t_, w_] /; FreeQ[b, t] := b fst[a, t, w]
fst[a_, t_, w_] := FourierSinTransform[a, t, w]
tset = fst[{eq, ic}, x, w] /. Rule @@ bc /.
HoldPattern@FourierSinTransform[a_, __] :> a
tsol = DSolve[tset, u[x, t], t][[1, 1, -1]]

The last step is to transform back. Assuming $p(t)$ is a nice enough function so that the order of integration can be interchanged:
With[{int = Inactive[Integrate]},
solfourier = tsol /.
coef_ int[a_, rest_] :>
int[InverseFourierSinTransform[coef a, w, x], rest]]

It's clear solfourier is equivalent to sol given that $k>0$. Solution verified, once again.

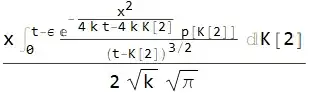







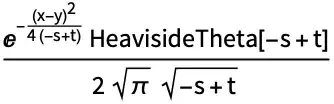

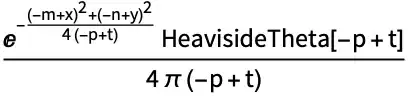

positive, which means $x>0$. In these problem, you just have to assume solution is valid, starting at just to the right ofx=0. So may be we can change the boundary condition to become $\lim_{\epsilon \to 0^+} x(\epsilon,t)=p(t)$ instead of $x(0,t)=p(t)$? I just verified Mathematica's solution in Maple also, and Maple gives the same exact solution, but only when assumingx>0as well. – Nasser Jun 13 '20 at 02:48