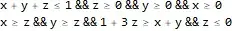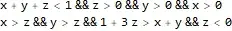Convert ConvexHull in a array to Inequality

Question

This question is in continuation with the previous post Convert ConvexHull to Inequality

There are two problems that I faced. Suppose we have two or more convex hull defined using an array R[i], like

P[0]={0,0,0};P[1]={1,0,0};P[2]={0,1,0};P[3]={0,0,1};P[4]={-1,-1,-1};P[5]={-1,0,-1};
P[6]={0,-1,-1};
R[1]=ConvexHullMesh[{P[0],P[1],P[2],P[3]}];
R[2]=ConvexHullMesh[{P[0],P[1],P[2],P[4]}];

Now to find the region inequality at once for all convex hull in the array I use a do loop as

    Do[regFunc[i][{x, y, z}] := FullSimplify @ RegionMember[Rationalize @ MeshPrimitives[DiscretizeRegion[R[i],  MaxCellMeasure -> \[Infinity]], 3][[1]]] @ {x, y, z},{i,1,2}];
regFunc[1]@{x,y,z}

But this gives error and so I have to manually write the whole code for each convex hull. Secondly, I want the region as a open region. This means that I want > or < not >= or <= . This is because later I will calculate region intersection using ImplicitRegion, where due to >= or <= the regions seem to intersect at the boundaries, which I don't want. Any possible way to do it in Mathematica?

score 3 · Accepted Answer · answered Jun 15 '20 at 03:44

The easy part of the question: (1) Use regFunc[i][{x_, y_, z_}] (not regFunc[i][{x, y, z}]) when you define regFunc, (2) Use With[{i = i}, ...] to inject the value of i on the right-hand-side expression:

Do[With[{i = i}, 
   regFunc[i][{x_, y_, z_}] := FullSimplify@
     RegionMember[
       Rationalize@
        MeshPrimitives[
          DiscretizeRegion[R[i], MaxCellMeasure -> ∞], 3][[1]]]@{x, y, z}],
   {i, 1, 2}];

Column @ {regFunc[1]@{x, y, z}, regFunc[2]@{x, y, z}}

Not sure about the second part, but maybe you can do this:

{regFunc[1]@{x, y, z}, regFunc[2]@{x, y, z}} /. 
     {LessEqual -> Less, GreaterEqual -> Greater} // Column

Convert ConvexHull in a array to Inequality

1 Answers1

Linked