I have a NonLinearModelFit in which a constraint is this formula (I have added the Print function to test)
ximgConst[xs_Real, xt_Real, alpha_Real, tao_Real] :=
Print@NIntegrate[(xt - xs)*(2*Pi*freq*tao)^(1 - alpha)*
Cos[alpha*Pi/2]/(1 +
2*(2*Pi*freq*tao)^(1 - alpha)*
Sin[alpha*Pi/2] + (2*Pi*freq*tao)^(2 - 2*alpha)), {freq, 0,
15000}, Method -> {Automatic, "SymbolicProcessing" -> 0}];
If I set the modelfit to MaxIterations->1 I am getting printed over 100 times different values per 1 iteration. Whenever I set my fit to 1000 iterations, this Integrate constraint slows down too much the fit.
Any clues? Thanks
Adding example code: Check how fast the fit is performed when the variable "PerformIntegral" is False, but it is broken when the variable becomes True. It makes no sense to me, when PerformIntegral = False the given result matches the integral constraint. But when the PerformIntegral = True there is no way I get a fast solution. Edit the code with the first code I gave and change the maxIterations to 1 and you'll see what I am speaking about
PerformIntegral = False;
dato = {{0, 100., 0.632135}, {1, 100., 0.145317}, {0, 300.,
0.473025}, {1, 300., 0.23012}, {0, 600., 0.344694}, {1, 600.,
0.234636}, {0, 1000., 0.256246}, {1, 1000., 0.211463}, {0, 2000.,
0.166665}, {1, 2000., 0.162959}, {0, 3000., 0.12934}, {1, 3000.,
0.133602}, {0, 4000., 0.107602}, {1, 4000., 0.113938}, {0,
5000., 0.0954281}, {1, 5000., 0.103238}, {0, 6000.,
0.0847213}, {1, 6000., 0.092765}, {0, 7000., 0.0781265}, {1,
7000., 0.0865319}, {0, 8000., 0.0712435}, {1, 8000.,
0.0791696}, {0, 9000., 0.0672512}, {1, 9000., 0.075166}, {0,
10000., 0.0628277}, {1, 10000., 0.0711438}} //
Rationalize[#, 0] &;
omtao1 = 2*Pi*freq*tao1;
omtao2 = 2*Pi*freq*tao2;
ximg1 = (xt1 - xs1)*omtao1^(1 - alpha1)*
Cos[alpha1*Pi/2]/(1 + 2*omtao1^(1 - alpha1)*Sin[alpha1*Pi/2] +
omtao1^(2 - 2*alpha1));
ximg2 = (xt2 - xs2)*omtao2^(1 - alpha2)*
Cos[alpha2*Pi/2]/(1 + 2*omtao2^(1 - alpha2)*Sin[alpha2*Pi/2] +
omtao2^(2 - 2*alpha2));
ximg = ximg1 + ximg2;
xreal1 = xs1 + (xt1 -
xs1)*(1 + omtao1^(1 - alpha1)*Sin[alpha1*Pi/2])/(1 +
2*omtao1^(1 - alpha1)*Sin[alpha1*Pi/2] + omtao1^(2 - 2*alpha1));
xreal2 = xs2 + (xt2 -
xs2)*(1 + omtao2^(1 - alpha2)*Sin[alpha2*Pi/2])/(1 +
2*omtao2^(1 - alpha2)*Sin[alpha2*Pi/2] + omtao2^(2 - 2*alpha2));
xreal = xreal1 + xreal2;
cole = ximg/xreal*xrealExp;
ximgConst[xs_?NumericQ, xt_?NumericQ, alpha_?NumericQ,
tao_?NumericQ] :=
NIntegrate[
Rationalize[(xt - xs)*(2*Pi*freq*tao)^(1 - alpha)*
Cos[alpha*Pi/2]/(1 +
2*(2*Pi*freq*tao)^(1 - alpha)*
Sin[alpha*Pi/2] + (2*Pi*freq*tao)^(2 - 2*alpha)), 0], {freq,
0, 15000}, Method -> {Automatic, "SymbolicProcessing" -> 0}];
xsinf1 = 0;
inixs1 = 0;
limxs1 = 14/10;
limxt1 = 2;
inixt1 = 6/10;
inialpha1 = 2/10;
initao1 = 2/100;
xsinf2 = 0;
inixs2 = inixs1;
limxs2 = limxs1;
limxt2 = limxt1;
inixt2 = inixt1;
inialpha2 = inialpha1;
initao2 = initao1;
actualPropProces = 1;
RealPropProces =
1/(1 + ximgConst[xs2, xt2, alpha2, tao2]/
ximgConst[xs1, xt1, alpha1, tao1]);
model = {(1 - set)*xreal +
set*ximg, {xsinf1 < xs1 < (limxs1 + 1/10)*5/2,
xs1 < xt1 < limxt1*5/2,
0 < alpha1 < Min[1, inialpha1*5], 0 < tao1 < Min[1, initao1*5], xt1 < xt2, xsinf2 < xs2 < (limxs2 + 1/10)*5/2, xs2 < xt2 < limxt2*5/2,
0 < alpha2 < Min[1, inialpha2*5], 0 < tao2 < Min[1, initao2*5],
If[PerformIntegral, RealPropProces < actualPropProces*11/10,
True]}} // Flatten;
fit = NonlinearModelFit[Rationalize[dato, 0], Rationalize[model, 0],
Rationalize[{{xs1, inixs1}, {xt1, inixt1}, {alpha1,
inialpha1}, {tao1, initao1}, {xs2, inixs2}, {xt2,
inixt2}, {alpha2, inialpha2}, {tao2, initao2}}, 0], {set, freq},
MaxIterations -> 10000, WorkingPrecision -> 22];
fit[[1, 2]]
"Prop: " <> ToString[RealPropProces /. fit[[1, 2]]]
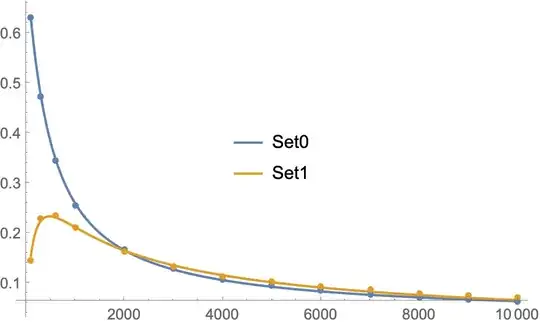
Show[Plot[Evaluate[fit[#, freq] & /@ {0, 1}], {freq, 100, 10000},
PlotRange -> All, PlotLegends -> Placed[{Set0, Set1}, {0.5, 0.5}]],
ListPlot[Map[Rest, GatherBy[dato, First], {2}]],
PlotRange -> {0, Max[dato[[All, 3]]]}]
NonlinearModelFitand yet your current example doesn't containNonlinearModelFit. – JimB Jun 17 '20 at 15:07ximgConst[xs_?NumericQ, xt_?NumericQ, alpha_?NumericQ, tao_?NumericQ]:= ...then an argument can also be an integer, rational, or numeric constant (e.g.,E,Pi) – Bob Hanlon Jun 17 '20 at 15:24