Inflection point coordinates of peaks in data

Question

Using the following data, which I have used before in other posts (the y-axis is heat flow (mW) and x-axis is Temperature in °C (not time)):

Import["https://pastebin.com/raw/SMKZUtbQ", "Package"]

which plotted using ListLinePlot[data, PlotRange -> {{50, 100}, {-0.1, 1}}] gives:

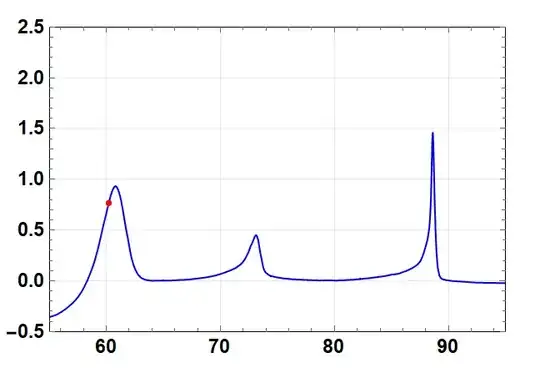
Question: How can I find the value (x and y coordinate) of the inflection(s) point to the left of each peak as shown in the figure (done with power point)?.

For this I have been using the code provided by MarcoB here: Find onset and peak temperatures

and additionally using the following approach:

start = 55;
end = 95;
region = Select[data, start <= #[[1]] <= end &];
fint = Interpolation[region];

which after using something like: infp = {x, fint[x]} /. FindRoot[fint''[x] == 0, {x, 59.4, 61}] finds the value {60.2085, 0.766843} which may be a possible inflection point for the first peak (left side) but it does not find all the inflection points of that peak. So, I am looking for a way to find the inflection(s) point(s) and a way to evaluate if they are indeed inflection(s) point(s).

Here's the point and the plot together using:

Show[Plot[fint[x], {x, start + 0.1, end - 0.1}, 
  PlotRange -> {{start, end}, {-0.5, 2.5}}, PlotStyle -> {Blue}, 
  AspectRatio -> aspect, Frame -> True, FrameStyle -> 14, 
  Axes -> False, GridLines -> Automatic, 
  GridLinesStyle -> Lighter[Gray, .8], 
  FrameTicks -> {Automatic, Automatic}, 
  LabelStyle -> {Black, Bold, 10}], 
 ListPlot[{infp}, PlotStyle -> Red]]

I appreciate your input

EDIT:

When I use infp = {x, fint[x]} /.FindRoot[fint''[x] == 0, {x, 59.8,61}] I find the following values {59.8211, 0.589037} which I check if this is a inflection point using (a very bad code):

belowinfp = fint''[infp[[1]] - 0.001]
aboveinfp = fint''[infp[[1]] + 0.001]

so that if belowinfp and aboveinfp have different signs, then I conclude that it is indeed an inflection point (in this case it is). If I used for instances infp = {x, fint[x]} /.FindRoot[fint''[x] == 0, {x, 59.4,61}] I find the values {60.2085, 0.766843} which using the same test I conclude that this is also an inflection point.

So, I guess the problem reduces to doing this automatically so that it will give me all the values of the inflections points using this test or any other.

Answer 1

Differentiating experimental data twice will blow up the noise, so you will probably need to smooth the data to get something usable. @halirutan's answer here applies a GaussianFilter to smooth the data.

To detect the zero crossings, we can use @Daniel Lichtblau's answer here.

The following workflow shows one possible approach that may point you in the right direction.

Import["https://pastebin.com/raw/SMKZUtbQ", "Package"]
start = 55;
end = 95;
region = Select[data, start <= #[[1]] <= end &];
fint = Interpolation[region];
(* Use halirutan's GaussianFilter answer to smooth data *)
ApplyGaussianFilter[data_, r_] := 
  Transpose[{#1, GaussianFilter[#2, r]}] & @@ Transpose[data];
data = ApplyGaussianFilter[data, 2];
(* Use BSplineFunction to Smooth and Resample Data on uniform x scale \
*)
bsf = BSplineFunction[data];
resampleddata = bsf[#] & /@ Subdivide[0, 1, 1000];
(* Create interpolation function *)
ifun = Interpolation[resampleddata, Method -> "Hermite"];
(* Use Daniel Lichtblau's Answer to Find Zeros using NDSolve *)
zeros = Reap[
    NDSolve[{y'[x] == D[ifun''[x], x], 
      WhenEvent[y[x] == 0, Sow[{x, y[x]}]], 
      y[start + 0.1] == ifun''[start + 0.1]}, {}, {x, start + 0.1, 
      end - 0.1}]][[-1, 1]];
pointsOnCurve = {#, ifun[#]} & /@ zeros[[All, 1]];
Plot[{fint[x], ifun[x]}, {x, start + 0.1, end - 0.1}, 
 Epilog -> {PointSize[Medium], Red, 
   Point[pointsOnCurve[[1 ;; -1 ;; 2]]], Green, 
   Point[pointsOnCurve[[2 ;; -1 ;; 2]]]}, PlotRange -> {-0.5, 1}]
Plot[{ifun[x], ifun''[x]}, {x, start + 0.1, end - 0.1}, 
 Epilog -> {PointSize[Medium], Red, Point[zeros[[1 ;; -1 ;; 2]]], 
   Green, Point[zeros[[2 ;; -1 ;; 2]]]}, PlotRange -> {-1, 1}, 
 PlotLabel -> "Smoothed"]
Plot[{fint[x], fint'''[x]}, {x, start + 0.1, end - 0.1}, 
 Epilog -> {PointSize[Medium], Red, Point[zeros[[1 ;; -1 ;; 2]]], 
   Green, Point[zeros[[2 ;; -1 ;; 2]]]}, PlotRange -> {-1, 1}, 
 PlotLabel -> "Unsmoothed"]

It did a pretty good job at detecting inflection points. Without smoothing, you get lots of false detections.

Answer 2

This is a testbed case for the function RegularisedInterpolation !

Import["https://pastebin.com/raw/SMKZUtbQ", "Package"]
fit = RegularisedInterpolation[data,
         FitRegularization->{"Curvature", 0.1}]

Show[
  ListPlot[data, PlotRange -> {{50, 100}, Automatic}],
  Plot[fit[x], {x, 50, 100},PlotStyle-> Directive[Red, Dashed]]
]

Thanks to the regularisation it can be differentiated twice.

d2fit[x_] = D[fit[x], x, x];
Plot[d2fit[x], {x, 60, 70}]

Then you can bracket the zeros:

FindRoot[d2fit[x] == 0, {x, 62, 64}]
FindRoot[d2fit[x] == 0, {x, 64, 66}]
(* 
 {x->62.3478}
 {x->64.4095} 
*) 

or use Daniel Lichtblau's zero crossings.

Validation

We can check that the result is fairly robust to the strength of smoothing

Table[
  fit = RegularisedInterpolation[data, 
    FitRegularization -> {"Curvature", 10^i}];
  d2fit[x_] = D[fit[x], x, x];
  x /. {FindRoot[d2fit[x] == 0, {x, 62, 64}],
  FindRoot[d2fit[x] == 0, {x, 64, 66}]},
  {i, -3, 1}]
(* {
{62.227,  64.4562},
{62.289,  64.4582},
{62.3478, 64.4095},
{62.3464, 64.413},
{62.2796, 64.4675}
} *)