In this topic we considering nonlinear ODE:
$\frac{dx}{dt}= (x^4) \cdot a_1 \cdot sin(\omega_1 \cdot t)-a_1 \cdot sin(\omega_1 \cdot t + \frac{\pi}{2})$ - Chini ODE
https://www.maplesoft.com/support/help/Maple/view.aspx?path=odeadvisor%2FChini
And system of nonlinears ODE:
$\frac{dx}{dt}= (x^4+y^4) \cdot a_1 \cdot sin(\omega_1 \cdot t)-a_1 \cdot sin(\omega_1 \cdot t + \frac{\pi}{2})$
$\frac{dy}{dt}= (x^4+y^4) \cdot a_2 \cdot sin(\omega_2 \cdot t)-a_2 \cdot sin(\omega_2 \cdot t + \frac{\pi}{2})$
Chini ODE's NDSolve in Mathematica:
pars = {a1 = 0.25, ω1 = 1}
sol1 = NDSolve[{x'[t] == (x[t]^4) a1 Sin[ω1 t] - a1 Cos[ω1 t], x[0] == 1}, {x}, {t, 0, 200}]
Plot[Evaluate[x[t] /. sol1], {t, 0, 200}, PlotRange -> Full]
System of Chini ODE's NDSolve in Mathematica:
pars = {a1 = 0.25, ω1 = 3, a2 = 0.2, ω2 = 4}
sol2 = NDSolve[{x'[t] == (x[t]^4 + y[t]^4) a1 Sin[ω1 t] - a1 Cos[ω1 t], y'[t] == (x[t]^4 + y[t]^4) a2 Sin[ω2 t] - a2 Cos[ω2 t], x[0] == 1, y[0] == -1}, {x, y}, {t, 0, 250}]
Plot[Evaluate[{x[t], y[t]} /. sol2], {t, 0, 250}, PlotRange -> Full]
There is no exact solution to these equations, therefore, the task is to obtain an approximate solution.
Using AsymptoticDSolveValue was ineffective, because the solution is not expanded anywhere except point 0.
The numerical solution contains a strong periodic component; moreover, it is necessary to evaluate the oscillation parameters. Earlier, we solved this problem with some users as numerically: Estimation of parameters of limit cycles for systems of high-order differential equations (n> = 3)
How to approximate the solution of the equation by the Fourier series so that it contains the parameters of the original differential equation in symbolic form, namely $a_1$, $\omega_1$, $a_2$ and $\omega_2$.
I would be grateful for any help!
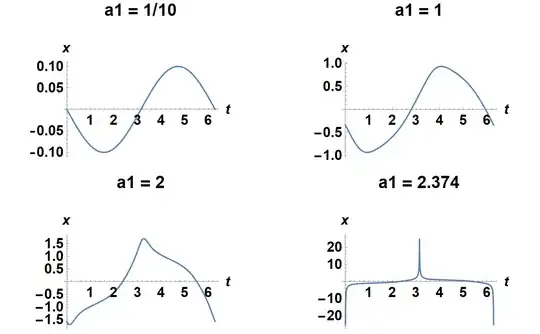
x[0] == 0gives a more obviously periodic solution to the first ODE, and that is what an FFT analysis is likely to yield. – bbgodfrey Jun 24 '20 at 12:45a1are you interested? The numerical solution becomes singular at about 2,374, requiring an infinite number of trig functions to represent. – bbgodfrey Jun 24 '20 at 20:23