I want to learn how to identify specific Christoffel Symbols and Riemman Tensor components from the general solution provided by Mathematica. Let us work out an example to see what I mean clearly.
Given the following metric
$g_{\mu \nu} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & r^2+b^2 & 0 & 0 \\ 0 & 0 & (r^2+b^2)\sin^2(\theta) & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} $
Using the following code
ChristoffelSymbol[g_, xx_] :=
Block[{n, ig, res}, n = Length[xx]; ig = Inverse[g];
res = Table[(1/2)*
Sum[ig[[i, s]]*(-D[g[[j, k]], xx[[s]]] + D[g[[j, s]], xx[[k]]] +
D[g[[s, k]], xx[[j]]]), {s, 1, n}], {i, 1, n}, {j, 1, n}, {k,
1, n}];
Simplify[res]]
(* The coordinates *)
xx = {r, θ, ϕ, t};
(* The metric *)
g = {{1, 0, 0, 0}, {0, r^2 + b^2, 0, 0}, {0,
0, (r^2 + b^2) Sin[θ]^2, 0}, {0, 0, 0, -1}};
ChristoffelSymbol[g, xx]
We get the general result
So how to identify from such general solution that the symbols are
$\Gamma^{1}_{22}=-r$
$\Gamma^{1}_{33}=-r\sin^2(\theta)$
$\Gamma^{2}_{21}=\frac{r}{b^2+r^2}$
$\Gamma^{2}_{33}=-\cos(\theta)\sin(\theta)$
$\Gamma^{3}_{31}=\frac{r}{b^2+r^2}$
$\Gamma^{3}_{32}=\cot(\theta)$
? (i.e. what code could we use?)
Same story with the Riemann Tensor;
Using the following code
RiemannTensor[g_, xx_] :=
Block[{n, Chr, res},
n = 4; Chr = ChristoffelSymbol[ g, xx];
res = Table[ D[ Chr[[i,k,m]], xx[[l]]]
- D[ Chr[[i,k,l]], xx[[m]]]
+ Sum[ Chr[[i,s,l]]*Chr[[s,k,m]], {s, 1, n}]
- Sum[ Chr[[i,s,m]]*Chr[[s,k,l]], {s, 1, n}],
{i, 1, n}, {k, 1, n}, {l, 1, n}, {m, 1, n}];
Simplify[ res]]
RiemannTensor[g, xx]
We get the general result
But how to identify the specific $R_{\mu \nu \rho \sigma}$ components?
EDIT 0
As Artes pointed out, the provided general solution for the Riemann Tensor is in the form $R^{\mu}_{\nu \sigma \rho}$.
What I really want is $R_{\mu \nu \sigma \rho}=g_{\mu\eta} R^{\eta}_{\phantom{\eta}\nu\sigma\rho}$ so I need to find a code that provides a general solution for the Riemann Tensor in the form $R_{\mu \nu \sigma \rho}$
I naively tried
g[[\[Mu],\[Eta]]]RiemannTensor[g,xx][[\[Eta],\[Mu],\[Sigma],\[Rho]]]
But this code simply yields the metric and $R^{\mu}_{\nu \sigma \rho}$ together, not $R_{\mu \nu \sigma \rho}$. Could somebody please provide the code that does the job? Thanks.
EDIT 1
First of all my apologies for not being clear enough in my original question.
My question is how to identify specific Christoffel symbols out of the general solution provided by Mathematica, which is the following
Imagine we're not given the values of the Christoffel symbols as in my original question. Then how can I know from the above solution that, for instance, $\Gamma^{1}_{22}=-r$?
I have the same issue with the Riemann tensor.

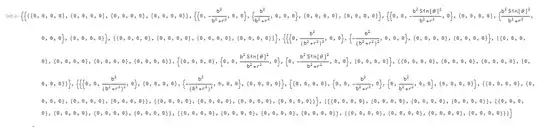
RiemannTensor[g, xx][[μ, ν, λ, σ]]represents $R^{\mu}{\phantom{\mu}\nu\lambda\sigma}=\partial{\lambda}\Gamma^{\mu}{\phantom{\mu}\nu\sigma}-\partial{\sigma} \Gamma^{\mu}{\phantom{\mu}\nu\lambda}+\Gamma^{\mu}{\phantom{\mu}\rho\lambda}\Gamma^{\rho}{\phantom{\mu}\nu\sigma}-\Gamma^{\mu}{\phantom{\mu}\rho\sigma}\Gamma^{\rho}_{\phantom{\mu}\nu\lambda}\quad$ – Artes Jun 23 '20 at 22:00