How do I convert a list to a Graph with directed edges?

Question

I created a discrete Markov process using p = DiscreteMarkovProcess[{1, 0, 0}, {{0, 1/2, 1/2}, {1/2, 0, 1/2}, {1/2, 1/2, 0}}]; and simulated it 5 times to create a list of lists:

data = Table[RandomFunction[p, {0, 10}][[2]][[1]][[1]], {i, 1, 5, 1}]
(*{{1, 3, 2, 1, 3, 1, 3, 1, 2, 1, 2}, {1, 2, 1, 2, 1, 2, 3, 2, 3, 2, 
  3}, {1, 3, 2, 1, 2, 3, 1, 2, 1, 3, 2}, {1, 3, 2, 1, 2, 1, 2, 1, 3, 
  1, 3}, {1, 2, 3, 1, 3, 1, 3, 2, 1, 2, 1}}*)

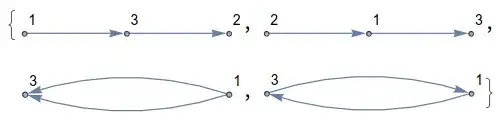
I would like to convert each of these lists into a list of vertices that are directed from the first member of the list to the next and then the next:

1 \[DirectedEdge] 3, 3 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 
 1 \[DirectedEdge] 3, 3 \[DirectedEdge] 1, 1 \[DirectedEdge] 3, 
 3 \[DirectedEdge] 1, 1 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 
 1 \[DirectedEdge] 2}

How do I do that? I explored EdgeAdd but that doesn't give me the desired result:

Table[EdgeAdd[
  Graph[{data[[1]][[1]] \[DirectedEdge] data[[1]][[2]]}, 
   VertexLabels -> "Name"], 
  data[[1]][[i]] \[DirectedEdge] data[[1]][[i + 1]]],
 {i, 2, 5, 1}]

What function may I use to convert a list to a set of directed vertices for a Graph?

score 6 · Answer 1 · answered Jun 24 '20 at 18:12

data =
  {{1, 3, 2, 1, 3, 1, 3, 1, 2, 1, 2}, {1, 2, 1, 2, 1, 2, 3, 2, 3, 2, 3}, {1, 3, 2, 
    1, 2, 3, 1, 2, 1, 3, 2}, {1, 3, 2, 1, 2, 1, 2, 1, 3, 1, 3}, {1, 2, 3, 1, 3, 1, 
    3, 2, 1, 2, 1}};

DirectedEdge @@@ Partition[#, 2, 1] & /@ data

{{1 \[DirectedEdge] 3, 3 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 
  1 \[DirectedEdge] 3, 3 \[DirectedEdge] 1, 1 \[DirectedEdge] 3, 
  3 \[DirectedEdge] 1, 1 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 
  1 \[DirectedEdge] 2}, {1 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 
  1 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 1 \[DirectedEdge] 2, 
  2 \[DirectedEdge] 3, 3 \[DirectedEdge] 2, 2 \[DirectedEdge] 3, 
  3 \[DirectedEdge] 2, 2 \[DirectedEdge] 3}, {1 \[DirectedEdge] 3, 
  3 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 1 \[DirectedEdge] 2, 
  2 \[DirectedEdge] 3, 3 \[DirectedEdge] 1, 1 \[DirectedEdge] 2, 
  2 \[DirectedEdge] 1, 1 \[DirectedEdge] 3, 
  3 \[DirectedEdge] 2}, {1 \[DirectedEdge] 3, 3 \[DirectedEdge] 2, 
  2 \[DirectedEdge] 1, 1 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 
  1 \[DirectedEdge] 2, 2 \[DirectedEdge] 1, 1 \[DirectedEdge] 3, 
  3 \[DirectedEdge] 1, 1 \[DirectedEdge] 3}, {1 \[DirectedEdge] 2, 
  2 \[DirectedEdge] 3, 3 \[DirectedEdge] 1, 1 \[DirectedEdge] 3, 
  3 \[DirectedEdge] 1, 1 \[DirectedEdge] 3, 3 \[DirectedEdge] 2, 
  2 \[DirectedEdge] 1, 1 \[DirectedEdge] 2, 2 \[DirectedEdge] 1}}

@dearN I think we all have those days; at least I do. :-) https://mathematica.stackexchange.com/a/71445/121 — Mr.Wizard, Jun 24 '20 at 18:16

score 6 · Accepted Answer · answered Jun 24 '20 at 18:12

6

If you have a list of vertices representing such a path, you can use

Graph[DirectedEdge @@@ Partition[list, 2, 1]]

If you just want the graph fort his Markov process, use Graph[p].

answered Jun 24 '20 at 18:12

Szabolcs

234,956
30
623
1,263

1

Beat you to the punch. ;^)) – Mr.Wizard Jun 24 '20 at 18:13
Oh my... this was simpler than expected. Silly me. Two answers at nearly the same time instance! – dearN Jun 24 '20 at 18:15
@Mr.Wizard 5 full seconds! :D I'll leave this though because of the Graph[p] bit, which I think many people don't know. (And +1) – Szabolcs Jun 24 '20 at 19:26

score 4 · Answer 3 · answered Jun 24 '20 at 20:07

You can also use BlockMap

toEdges1 = BlockMap[Apply @ DirectedEdge, #, 2, 1] &;

or the (undocumented) 6-argument form of Partition:

toEdges2 = Partition[#, 2, 1, {1, -1}, {}, DirectedEdge] &;

Using it with data:

toEdges1 /@ data

Row[Graph[#, ImageSize -> 200] & /@ toEdges1 /@ data]

toEdges1 /@ data == 
    toEdges2 /@ data == 
     ( DirectedEdge @@@ Partition[#, 2, 1] & /@ data)

 True

How do I convert a list to a Graph with directed edges?

3 Answers3