How to get rid of imaginary part in cubic root

Question

When I try to solve the following cubic equation for $a$ on mathematica :

S=Solve[a^3 - 4 x - 2 a^2 x + 8 x^3 + a (- 6 - 4 x^2) == 0,a];

I get a complex expression for the root I am interested in (accessible in S[[3,1,2]]) :

root[x_]:=1/12 (8 x + (
   4 (-2)^(2/3) (9 + 8 x^2))/(54 x - 32 x^3 + 
     3 I Sqrt[6] Sqrt[27 + 2 x^2 (9 + 64 x^2)])^(1/3) - 
   4 (-2)^(1/
     3) (54 x - 32 x^3 + 3 I Sqrt[6] Sqrt[27 + 2 x^2 (9 + 64 x^2)])^(
    1/3))

It is a valid expression for the root :

FullSimplify[root[x]^3 - 4 x - 2 root[x]^2 x + 8 x^3 + root[x] (- 6 - 4 x^2)]==0

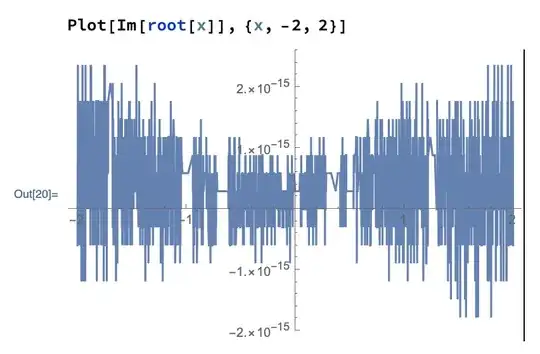
However the root is real, but Mathematica believes there is a very small imaginary part :

Plot[root[x],{x,-2,2}]

How can I get rid of the imaginary part of my solution ? I have tried commands such as Re@ComplexExpand[root[x]] But it gives very tedious expressions to work with. From the context of the project I am working on I firmly believe there exist a much nicer expression for root[x].

I am open for any ideas or remarks, thank you very much.

Just increase the working precision for plot - you're seeing an artifact of plot's use of inexact numbers in sampling plot points. — ciao, Jun 24 '20 at 19:28

score 4 · Answer 1 · answered Jun 24 '20 at 19:22

Why not work with Root objects instead? Consider:

S=Solve[a^3-4 x-2 a^2 x+8 x^3+a (-6-4 x^2)==0,a];
S /. x->3.

{{a -> 8.07232 + 0. I}, {a -> -6.16892 - 4.44089*10^-16 I}, {a -> 4.09659 + 0. I}}

Compared to:

T=Solve[a^3-4 x-2 a^2 x+8 x^3+a (-6-4 x^2)==0, a, Cubics->False];
T /. x->3.

{{a -> -6.16892}, {a -> 4.09659}, {a -> 8.07232}}

So, the Root expression corresponding to your desired root is:

root = a /. T[[2]]

Root[-4 x + 8 x^3 + (-6 - 4 x^2) #1 - 2 x #1^2 + #1^3 &, 2]

Check that the root has zero imaginary part:

Plot[Im @ root, {x, -2, 2}]

As further evidence that the imaginary part is zero, T is identical to the solution obtained if the solution is restricted to the real domain, i.e., T === Solve[a^3 - 4 x - 2 a^2 x + 8 x^3 + a (-6 - 4 x^2) == 0, a, Reals] evaluates to True — Bob Hanlon, Jun 24 '20 at 20:03

score 0 · Answer 2 · answered Jun 24 '20 at 20:24

First, the solutions are real only if x is real. In that case, here's a way to simplify the third solution in S to a real expression:

realSimple = Simplify[#, x ∈ Reals] &;
s1 = a /. S[[3]] // ComplexExpand // realSimple
(*
1/3 (2 x - 
   Sqrt[2] Sqrt[9 + 8 x^2]
     Cos[1/3 Arg[54 x - 32 x^3 + 3 I Sqrt[6] Sqrt[27 + 18 x^2 + 128 x^4]]] + 
   Sqrt[6] Sqrt[9 + 8 x^2]
     Sin[1/3 Arg[54 x - 32 x^3 + 3 I Sqrt[6] Sqrt[27 + 18 x^2 + 128 x^4]]])
*)

Arg is real-valued, but we can go further. Note the imaginary part of the argument to Arg is positive, so that Arg[] will lie between 0 and Pi.

s2 = s1 /. (A_ : 1) Cos[t_] + (B_ : 1) Sin[t_] :> 
     Sqrt[A^2 + B^2] Cos[t - ArcTan[A, B]] /. 
   Arg :> (Pi/2 - ArcTan[Re@#/Im@#] &) // realSimple
(*
2/3 (x - Sqrt[2] Sqrt[9 + 8 x^2]
     Sin[1/3 ArcTan[(54 x - 32 x^3)/(3 Sqrt[6] Sqrt[27 + 18 x^2 + 128 x^4])]])
*)

For related Q&A, see How do I get the solutions of a cubic equation in trigonometric form? and its linked questions.

How to get rid of imaginary part in cubic root

2 Answers2