How to draw a surface in polar coordinates

Question

I want to draw a figure in this post, but the result that I draw according to the following method is quite different from that in the post.

ParametricPlot3D[{r Cos[θ], r Sin[θ], 
  r^2*4 Mod[(1/r - θ/(2 π)), 
    1] (1 - Mod[(1/r - θ/(2 π)), 1])}, {θ, 0, 
  2 π}, {r, 0, 1}, PlotPoints -> 25, BoxRatios -> {1, 1, 1}, 
 PlotRange -> {-1, 1}]

3D plots

How can I draw a graph which is basically the same as the above one?

score 7 · Accepted Answer · answered Jun 28 '20 at 15:18

The plots that you are trying to reproduce appear to use Plot3D rather than ParametricPlot3D

Clear["Global`*"]
g[r_, θ_] := Module[
  {t = Mod[1/r - θ/(2 π), 1]}, 4 t (1 - t)]
plt1 = With[{r = Sqrt[x^2 + y^2], θ = ArcTan[x, y]},
   Plot3D[r^2*g[r, θ], {x, -1, 1}, {y, -1, 1},
    PlotPoints -> 200,
    PlotRange -> {{-1, 1}, {-1, 1}, {0, 1.9}},
    Mesh -> None,
    Exclusions -> None,
    AxesLabel -> Automatic]];
plt2 = With[{r = Sqrt[x^2 + y^2], θ = ArcTan[x, y]},
   Plot3D[g[r, θ], {x, -1, 1}, {y, -1, 1},
    PlotPoints -> 200,
    PlotStyle -> Opacity[0.75],
    PlotRange -> {{-1, 1}, {-1, 1}, {0, 1}},
    Mesh -> None,
    Exclusions -> None,
    AxesLabel -> Automatic]];
GraphicsRow[{plt1, plt2}]

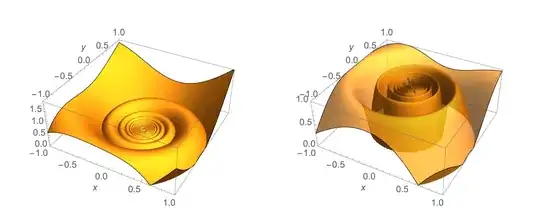
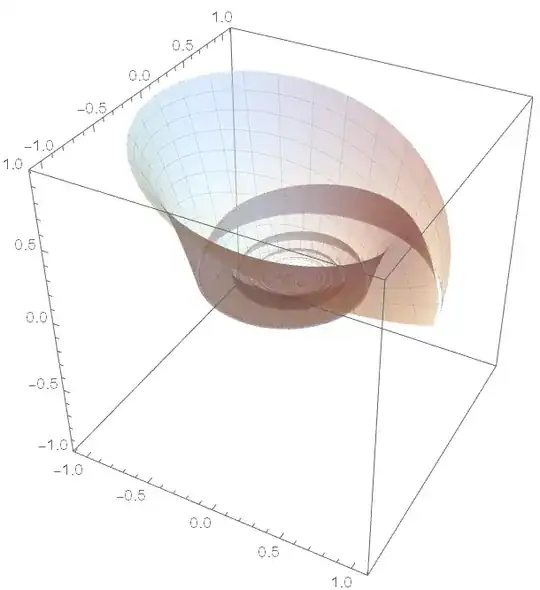
PlotTheme -> "Classic" if you want the old school look. – flinty Jun 29 '20 at 12:43 — flinty, Jun 29 '20 at 12:43

score 1 · Answer 2 · answered Jun 28 '20 at 15:10

Adding the following styling options gets you closer, but you will have to experiment to get your desired effect:

ParametricPlot3D[{r Cos[θ], r Sin[θ], 
  r^2*4 Mod[(1/r - θ/(2 π)), 
    1] (1 - Mod[(1/r - θ/(2 π)), 1])}, {θ, 0, 
  2 π}, {r, 0, 1}, PlotPoints -> 50, BoxRatios -> {1, 1, 1}, 
 PlotRange -> {-1, 1}, Mesh -> 25, 
 MeshStyle -> Directive[Gray, Opacity[0.2]], PlotPoints -> 75, 
 PlotStyle -> Directive[LightBlue, Opacity[0.5]], 
 PerformanceGoal -> "Quality"]

How to draw a surface in polar coordinates

2 Answers2