Deformation following loads in AceFEM/AceGen

Question

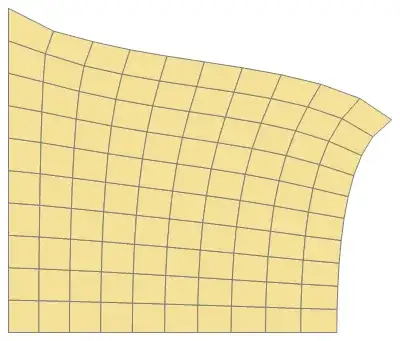
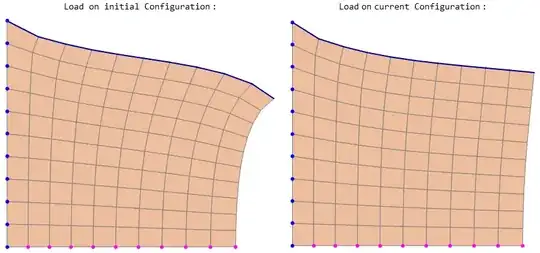
I have a simple 2D finite element problem comprising a unit domain that is fully constrained on the left, vertically constrained on the bottom and subject to a uniformly distributed load at the top. See below

At present the load remains vertical throughout the deformation. How can I modify this problem so that the load follows the deformation and stays perpendicular to the top surface of the body?

My current code is shown below

(* Open AceFEM *)
<< AceFEM`;
(* Domain and load *)
DensityX = 10;
DensityY = 10;
Height = 1;
Width = 1;
Load = -50;
SMTInputData["Threads" -> 4];
(* Create domain *)
SMTAddDomain[
  "CornerDomain", {"ML:", "SE", "PE", "Q1", "DF", "HY", "Q1", 
   "D", {{"NeoHooke", "WA"}}}, {"E *" -> 200}];
SMTMesh["CornerDomain", 
  "Q1", {DensityX, 
   DensityY}, {{{0, 0}, {Width, 0}}, {{0, Height}, {Width, Height}}}];
(* Boundary conditions *)
SMTAddEssentialBoundary["X" == 0 &, 1 -> 0, 2 -> 0];
SMTAddEssentialBoundary["Y" == 0 &, 2 -> 0];
SMTAddNaturalBoundary[Line[{{0, Height}, {Width, Height}}], 
  2 -> Line[{Load}]];
(* Begin analysis *)
SMTAnalysis[];
SMTShowMesh["BoundaryConditions" -> True]
(* Solution procedure *)
tolNR = 10^-5; maxNR = 500; targetNR = 100;
λMax = 1; λ0 = λMax/1000; 
ΔλMin = λMax/10000; ΔλMax = λMax/100;
SMTNextStep["λ" -> λ0];
While[
  While[
   step = 
    SMTConvergence[tolNR, 
     maxNR, {"Adaptive BC", 
      targetNR, ΔλMin, ΔλMax, λMax}]
   , SMTNewtonIteration[];
   ];
  If[step[[4]] === "MinBound", SMTStatusReport["Analyze"]; 
   SMTStepBack[];];
  step[[3]] 
  , If[step[[1]], SMTStepBack[];];
  SMTNextStep["Δλ" -> step[[2]]]
  ];

Which yields the deformed body

Any help would be appreciated!

You can find example of this in AceFEM documentation, in the notebook "Gas Pressure Element - Inflating the Tyre". Chapter in Korelc book "6.2.3 Deformation Dependent Loads" may be also interesting for you. — Pinti, Jul 06 '20 at 18:42

score 7 · Accepted Answer · edited Jul 07 '20 at 16:34

There are multiple ways to do what you want, but the simplest one is to define a load element in AceGen and integrate load on the deformed configuration instead of initial.

Here is a simple working load element on current configuration:

<< AceFEM`;
<< AceGen`;
SMSInitialize["LoadFollowingL1", "Environment" -> "AceFEM"];
SMSTemplate["SMSTopology" -> "L1", 
  "SMSDomainDataNames" -> {"qX -area load, X direction", 
    "qY -area load, Y direction", "qT -traction load", 
    "qN -normal load", "t -thickness"}, 
  "SMSDefaultData" -> {0, 0, 0, 0, 1}];
Discretization[] := ({ξ, η, ζ, wgp} ⊢ 
   Array[SMSReal[es$$["IntPoints", #1, Ig]] &, 
4]; Ξ = {ξ, η, ζ};
  {qX, qY, qT, qN, th} ⊢ 
   SMSReal[Table[es$$["Data", i], {i, Length[SMSDomainDataNames]}]];
  Nh ⊨ {(1 - ξ)/2, (1 + ξ)/2};
  XIO = SMSReal[
    Table[nd$$[i, "X", j], {i, SMSNoNodes}, {j, SMSNoDimensions}]];
  uIO = SMSReal[
Table[nd$$[i, "at", j], {i, SMSNoNodes}, {j, SMSDOFGlobal[[i]]}]];
  u ⊨ PadRight[Nh.uIO, 3];
  SMSFreeze[X, PadRight[Nh.XIO, 3, Ξ] + u];
  gξ ⊨ SMSD[X[[;; SMSNoDimensions]], ξ];
  gη ⊨ {-ξ[[2]], ξ[[1]]};
  gξn ⊨ SMSSqrt[gξ.gξ];
  tξ ⊨ gξ/gξn;
  tη ⊨ {-tξ[[2]], tξ[[1]]};
  FGauss ⊢ th gξn;
  [DoubleStruckP]e ⊨ Flatten[uIO];
  λ ⊨ SMSReal[rdata$$["Multiplier"]];
  P ⊢ 
   PadRight[{qX, qY} + {tξ, tη}[Transpose].{qT, qN}, 3, 0];
  pseudoWConstants = {P, FGauss};
  W = -λ P.u;)
SMSStandardModule[FEMModule = "Tangent and residual"];
NoIp ⊨ SMSInteger[es$$["id", "NoIntPoints"]];
SMSDo[Ig, 1, NoIp];
Discretization[];
SMSDo[i, 1, Length[[DoubleStruckP]e]];
Rgi ⊨ 
  wgp FGauss SMSD[W, [DoubleStruckP]e, i, 
    "Constant" -> SMSVariables[pseudoWConstants]];
SMSExport[Rgi, p$$[i], "AddIn" -> True];
SMSDo[j, If[SMSSymmetricTangent, i, 1], Length[[DoubleStruckP]e]];
Kgij ⊨ SMSD[Rgi, [DoubleStruckP]e, j];
SMSExport[Kgij, s$$[i, j], "AddIn" -> True];
SMSEndDo[];
SMSEndDo[];
SMSEndDo[];
SMSWrite[];

The only lines needed to modify standard load elements, that will ensure the integration on current configuration is by using current coordinates: X+u instead just X:

SMSFreeze[X,PadRight[Nh.XIO,3,Ξ]+u];

also both Load and the weight have to be set constant during differentiation of potential W i.e.

pseudoWConstants = {P, FGauss};
Rgi ⊨ wgp FGauss SMSD[W, \[DoubleStruckP]e, i, "Constant" -> SMSVariables[pseudoWConstants]];

We just have to be sure that P and FGauss are AceGen symbols, so we should define them with ⊢. Then you just use the element in AceFEM by defining Load domain and mesh:

SMTAddDomain["Load","LoadFollowingL1",{"qN *"->Load}];
SMTMesh["Load","L1",{DensityX},{{0,Height},{Width,Height}}];

And remove the SMTAddNaturalBoundary And you get solution:

This load is guided through the multiplier, you can modify element to have constant load also by redefining the potential as: W = -(λ P + P0).u, if needed, where P0 is same as P but with new set of element domain data.

Do you have an idea how to solve this question? – user21 Jul 15 '21 at 09:32 — user21, Jul 15 '21 at 09:32

Deformation following loads in AceFEM/AceGen

1 Answers1