0

Can anybody help me to plot the T1 and T2, please?

The problem is that the integral part becomes so huge or indeterminate at some points. So how do I find and skip such points?

b = (2.3*10^16)/(2.5*10^6*2.1*10^4)*(2.5*10^6 + 2.1*10^4 + (2.5*10^6)/(2.3*10^16)*2.1*10^4*(y/(100*2.5*10^-9))^2)
d = Sqrt[b^2 - 4*315*(y/(100*2.5*10^-9))^2*(2.3*10^16)/(2.5*10^6*2.1*10^4)]
p1 = -(b - d)/2
p2 = -(b + d)/2
T1 = (1.58*10^-5*2.3*10^16*10^-15)/((2*π)^1.5*0.84*2.5*10^-18*10^-15*2.5*10^6*2.1*10^4)*Sqrt[π/2]*NIntegrate[BesselJ[0, y]/Sqrt[(y^2 + 100^2)^3]*1/d*((1 - Erf[(p1*10^-15 - 1)/Sqrt[2]])*Exp[(p1*10^-15)^2/2 - p1*10^-15*(1 - t)] - (1 -Erf[(p2*10^-15 - 1)/Sqrt[2]])*Exp[(p2*10^-15)^2/2 - p2*10^-15*(1 - t)])*y*50, {y, 0, ∞}]
T2 = T1 + (1.58*10^-5*10^-15)/((2*π)^1.5*0.84*2.5*10^-18*10^-15*2.1*10^4)*Sqrt[π/2]*NIntegrate[BesselJ[0, y]/Sqrt[(y^2 + 100^2)^3]*1/d*(p1*(1 - Erf[(p1*10^-15 - 1)/Sqrt[2]])*Exp[(p1*10^-15)^2/2 - p1*10^-15*(1 - t)] - p2*(1 - Erf[(p2*10^-15 - 1)/Sqrt[2]])*Exp[(p2*10^-15)^2/2 - p2*10^-15*(1 - t)])*y*100, {y, 0, ∞}]
Plot[T1, {t, 0.01, 6000}]  
Plot[T2, {t, 0.01, 6000}]

If I write T1 and T2 like T1=Ta+Tb, T2=T1+Tc+Td (evaluationg integral members separately) it works in V5:

b = (2.3*10^16)/(2.5*10^6*2.1*10^4)*(2.5*10^6 + 2.1*10^4 + (2.5*10^6)/(2.3*10^16)*2.1*10^4*(y/(100*2.5*10^-9))^2)
d = Sqrt[b^2 - 4*315*(y/(100*2.5*10^-9))^2*(2.3*10^16)/(2.5*10^6*2.1*10^4)]
p1 = -(b - d)/2
p2 = -(b + d)/2
Ta = (1.58*10^-5*2.3*10^16*10^-15)/((2*π)^1.5*0.84*2.5*10^-18*10^-15*2.5*10^6*2.1*10^4)*Sqrt[π/2]*NIntegrate[BesselJ[0, y]/Sqrt[(y^2 + 100^2)^3]*1/d*((1 - Erf[(p1*10^-15 - 1)/Sqrt[2]])*Exp[(p1*10^-15)^2/2 - p1*10^-15*(1 - t)])*y*100, {y, 0, ∞}]

Tb = (1.5810^-52.310^1610^-15)/((2π)^1.50.842.510^-1810^-152.510^62.110^4)Sqrt[π/2]NIntegrate[BesselJ[0, y]/Sqrt[(y^2 + 100^2)^3]1/d(-(1 -Erf[(p210^-15 - 1)/Sqrt[2]])Exp[(p210^-15)^2/2 - p210^-15(1 - t)])y100, {y, 0, ∞}]


Tc = (1.5810^-510^-15)/((2π)^1.50.842.510^-1810^-152.110^4)Sqrt[π/2]NIntegrate[BesselJ[0, y]/Sqrt[(y^2 + 100^2)^3]1/d(p1(1 - Erf[(p110^-15 - 1)/Sqrt[2]])Exp[(p110^-15)^2/2 - p110^-15*(1 - t)])y100, {y, 0, ∞}]
Td = (1.5810^-510^-15)/((2π)^1.50.842.510^-1810^-152.110^4)Sqrt[π/2]NIntegrate[BesselJ[0, y]/Sqrt[(y^2 + 100^2)^3]1/d(-p2(1 - Erf[(p210^-15 - 1)/Sqrt[2]])Exp[(p210^-15)^2/2 - p210^-15*(1 - t)])y100, {y, 0, ∞}]
Plot[Ta+Tb, {t, 0.01, 6000}]

Plot[Ta+Tb+Tc+Td, {t, 0.01, 6000}]

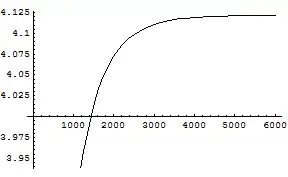
T1:

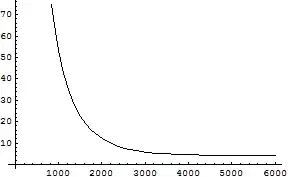
enter image description here

T2:

enter image description here

Obviously, some points are missing, but it is still helpful. At least, I can say that my calculation are correct :)

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Ismatov Tolib
  • 63
  • 4
  • You have (1 - t) in your integrals, but t is neither defined, nor the variable of integration. On top of that the integral is highly oscillatory, but the (1-t) issue needs fixing first. – flinty Jul 04 '20 at 20:29
  • @flinty It seems t is the parameter, see Plot[T1, {t, 0.01, 6*10^3}] – yarchik Jul 04 '20 at 20:35
  • 1
    Since you're plotting over t, you should change T1,T2 into functions of t so replace T1 and T2 with T1[t_?NumericQ] := ... and T2[t_?NumericQ] := T1[t] + .... That fixes problem 1. The remaining problem is that now we can evaluate T1, we have T1[2.0] giving 7.209952984984601*10^37881 which is huge and off the scale. – flinty Jul 04 '20 at 20:35
  • @Bill yes, as I increase y-perameter, T1 becomes so huge OR indeterminate at some points as FLINTY mentioned previously. So, how to skip that points? Maybe by considering low precision or some approximations :-( – Ismatov Tolib Jul 04 '20 at 23:14
  • I don't think this is a problem that can be resolved by skipping a few points when plotting, if T1 and T2 should not be so huge, their definitions need to be doube-checked. BTW this time the code doesn't even work in v5. – xzczd Jul 05 '20 at 03:10
  • @xzczd it works in V5 when T1 is evaluated seperately. Like: T1=Ta-Tb Ta=...Nintegrate[F[p1]...] Tb=...Nintegrate[F[p2]...] Plot[Ta-Tb]. T2 is also works when evaluated in this manner but only in V5. I discovered this actually by coincidence. So can anybody explain what is the difference between V5 and new versions? – Ismatov Tolib Jul 05 '20 at 17:20
  • Then please show us the code works in v5. – xzczd Jul 06 '20 at 11:53
  • @xzczd I added the code at the endof the post – Ismatov Tolib Jul 06 '20 at 14:43
  • 1
    I've updated my previous answer, the new added solution works for your new problem now. Notice you need to adjust the domain of t to e.g. {t, 500, 6*10^3}. – xzczd Jul 07 '20 at 02:58

0 Answers0