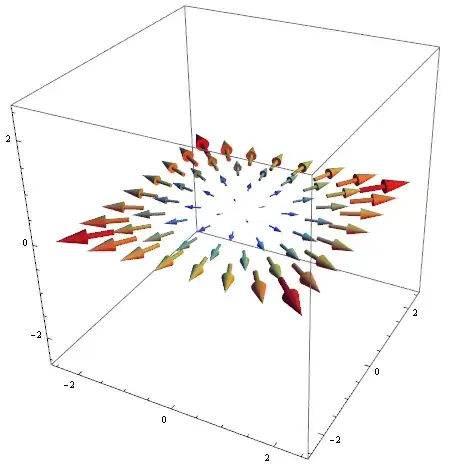
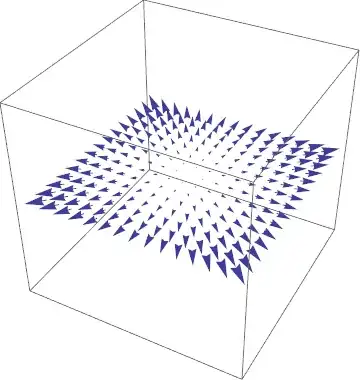
I want to plot a 2D vector function such as $F(x,y) = (a(x,y),\,b(x,y))$ in a 3D graph so that the vectors are embedded in the xy plane. I tried to do the following:
First I defined a piecewise function like this
g[z_] := Piecewise[{{1, z == 0}}, 0]
Then I converted the 2D vector function to a 3D one by setting the 3rd component to zero and multiplying 1st and 2nd components by g[z] so that the x and y components are null when z != 0:
f[x_, y_, z_] := {x g[z], y g[z], 0};
Plot the function:
VectorPlot3D[{x g[z], y g[z],0}, {x, -5, 5}, {y, -5, 5}, {z, -5, 5}]
The issue with this solution is that VectorPlot3D won't evaluate the function in the relevant points, The above example shows an empty graph, because Mathematica jumps from z = -1 to z = 1 without evaluating z = 0.
I tried with RegionFunction (which would've rendered the definition of the above-mentioned piecewise function useless), but that only accepts inequalities, and I want to evaluate the function at any coordinate {x ,y, 0}.
I could feed it a list of vectors via VectorPoints -> { {a, b, 0}, {c, d, 0}, ...}, but that's not an elegant solution at all. Are there other ways to do this?
Read the FAQs! 3) When you see good Q&A, vote them up byclicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. ALSO, remember to accept the answer, if any, that solves your problem,by clicking the checkmark sign` – Vitaliy Kaurov Apr 02 '13 at 23:33