0

Here is the code.

Solve[(1 - E^x + (3 x^2)/2)/(2 x) == a, x, Reals]

Unfortunately, Mathematica told me that this system cannot be solved with the methods available to Solve. If not a symbolic relation, can a numeric relation be found?

What's the numeric relation of x expressed in terms of a?

Let's make up a numeric relation between $x$ and $a$.

$x \rightarrow 0.812a+\frac{1}{2}a^2 $

Anyone who have a better idea?

kile
  • 1,671
  • 5
  • 10
  • 1
    Similar questions were asked and answered a lot here. Try the numeric approach:f[a_] := NSolve[(1 - E^x + (3 x^2)/2)/(2 x) == a, x, Reals];f[-1] which results in {{x -> -0.892312}, {x -> 3.04378}}. Even AsymptoticSolve[(1 - E^x + (3 x^2)/2)/(2 x) == a, {x}, {a, -1, 2}] fails. – user64494 Jul 11 '20 at 06:41
  • @user64494, why is there not a symbolic answer? Can you explain it? – kile Jul 11 '20 at 09:12
  • 2
    @kile Transcendental equations generally do not yield to analytic closed-form solutions. They may do so sometimes when one of the independent variable tends to some limit (like $\rightarrow 0$ or $\rightarrow \infty$). You can find an example here – Avrana Jul 11 '20 at 09:28
  • 1
    This post should clarify your doubts What is the difference between Reduce and Solve?. In fact, given a numeric value to a < -0.03475 you can find solution with Solve. – Artes Jul 11 '20 at 09:53
  • 1
    @Artes, is it possible to find the relation between x and a? For example, x=0.813a+0.7 a^2 – kile Jul 11 '20 at 10:19

4 Answers4

3

Not an answer, just a long comment.

By making small Manipulate, it shows that no real solution exist when $a$ gets over value of around $-1/10$. Hard to determine the exact value of $a$ but using the slider you can get very close to finding it. i.e when $a$ is larger than that limit, it never crosses the x-axis, so no real solution exist.

ClearAll[a,x];
eq = (1 - Exp[x] + (3 x^2)/2)/(2 x) - a;
Manipulate[Plot[eq /. a -> a0, {x, -3, 3}],
 {{a0, 0, "a"}, -1, 1, .001, Appearance -> "Labeled"},
 TrackedSymbols :> {a0}
 ]

enter image description here

I think this might explain why Solve could not do it in addition to the other comments above.

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • Is it possible to find the relation between "a" and "x"? Like x= 0.813a + a^2 – kile Jul 11 '20 at 10:17
  • @kile well, the relation is the equation itself? which is echoed back when you type Solve[(1 - E^x + (3 x^2)/2)/(2 x) == a, {a, x}, Reals] Make sure to add a in Solve here. – Nasser Jul 11 '20 at 10:22
  • 1
    That's what I get when input your code. a -> 1/4 (2/x - (2 E^x)/x + 3 x). Still, This is not what I want. what I want is x->...a is expressed in terms of a. – kile Jul 11 '20 at 10:31
  • 1
    @kile Ok, misunderstood you. There is no equation to solve for $x$ in terms of $a$ I am afraid. If you try by hand, you'll see why. The equation is not polynomial so no exact formula exist. If you have specific numerical value for a, it can do it. – Nasser Jul 11 '20 at 10:38
2

Well if you insist on having some relation you can always use FindFormula note that from an analytic perspective this is not the "correct" answer.

sols = Table[
   Flatten@{a, 
     x /. Solve[(1 - E^x + (3 x^2)/2)/(2 x) == -a, x, Reals]}, {a, 1, 
    100}];
branch1 = sols[[All, {1, 2}]];
branch2 = sols[[All, {1, 3}]];
formula1 = FindFormula[branch1, a];
formula2 = FindFormula[branch2, a];

Now you have some formulas formula1 and formula2 which might be helpful or not.

Natas
  • 2,310
  • 4
  • 14
  • 1
    It is funny---some formulas... In what domain are they accurate? – yarchik Jul 11 '20 at 13:47
  • Well, you can choose the domain of accuracy by setting the range of a in the definition of sols. I am not sure about this problem, but in general the solutions will be only valid in that domain and complete nonsense outside. – Natas Jul 11 '20 at 13:48
2
$Version

(* "12.1.1 for Mac OS X x86 (64-bit) (June 19, 2020)" *)

Clear["Global`*"]

eqn = (1 - E^x + (3 x^2)/2)/(2 x) == a;

The numeric solution for a given value of a and an initial estimate is given by FindRoot

f[a_?NumericQ, init_?NumericQ] :=
 FindRoot[(1 - E^x + (3 x^2)/2)/(2 x) == a, {x, init}]

pt1 = ({x, a} /. f[a, -10]) /. a -> -6 // Quiet


(* {-7.91581, -6} *)


pt2 = ({x, a} /. f[a, 3]) /. a -> -6 // Quiet


(* {4.42428, -6} *)

To find the max value of a

xa = Solve[D[eqn[[1]], x] == 0, x, Reals][[1]]

(* {x -> Root[{-2 + E^#1(2 - 2#1) + 
             3#1^2 & , 
    1.554653058468533267935

     17428741457642172`20.286009576768794}]} )

The exact value is a Root expression.

The maximum value of a is then

amax = a /. Solve[eqn /. xa, a, Reals][[1]]

(* (1 - E^Root[{-2 + E^#1(2 - 2#1) + 
                3#1^2 & , 
      1.55465305846853326793

       517428741457642172`20.286009576768794}] + 
      (3/2)Root[{-2 + E^#1(2 - 2#1) + 
                  3#1^2 & , 
       1.5546530584685332679

        3517428741457642172`20.286009576768794}]^
          2)/(2Root[{-2 + E^#1(2 - 2#1) + 
              3#1^2 & , 
     1.554653058468533267935

      17428741457642172`20.286009576768794}]) )

The {x, a} point for max a is

(pt = {x, amax} /. xa) // N

(* {1.55465, -0.0347424} *)

where N has converted the Root expressions to their approximate numeric values.

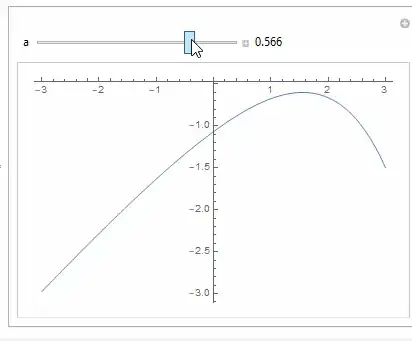
ContourPlot shows the solutions to the equation

ContourPlot[Evaluate@eqn, {x, -13, 5}, {a, -10, 0},
 PlotPoints -> 50,
 Epilog -> {AbsolutePointSize[4], Tooltip[Point[#], #] & /@ {pt1, pt2},
   Red, Tooltip[Point[#], #] &[N@pt]},
 FrameLabel -> (Style[#, 14, Bold] & /@ {x, a})]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
0

You can use AsymptoticSolve to get a solution near x=k as following:

    AsymptoticSolve[(1 - E^x + (3 x^2)/2)/(2 x) == a, {x, k}, {a, (1 - E^k + (3 
    k^2)/2)/(2 k), 2}]

(*{{x -&gt; k + (4 k^2 (a - (1 - E^k + (3 k^2)/2)/(2 k)))/(-2 + 2 E^k - 2 E^k k + 



3 k^2) + (16 k^3 (-2 + 2 E^k - 2 E^k k + E^k k^2) (a - (1 - E^k + (3 k^2)/2)/(2 k))^2)/(-2 + 2 E^k - 2 E^k k + 
  3 k^2)^3}}*)
Jie Zhu
  • 513
  • 2
  • 9