I'd like to connect many spheres, by adding a new sphere at some point that's sitting on the surface of a previous sphere. How could we do this?
Suppose I have a unit sphere and a point on it:
myShpere1=Sphere[];
myPoint1=SpherePoints[1];
Graphics3D[{myShpere1, Point[myPoint1]}]
How can we add a second sphere who's surface is touching the previous one at the random point, then a third sphere on a random point of the second sphere, and so on? (for any number of spheres, always choosing a new random point). On a related issue, do spheres have an orientation in MMA, as ellipsoids do? If so, how do we get the "vector/axis" of orientation?
Thanks!

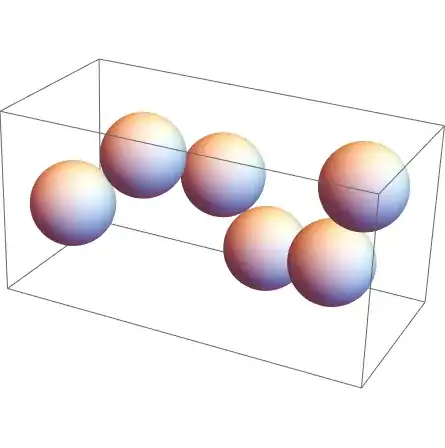
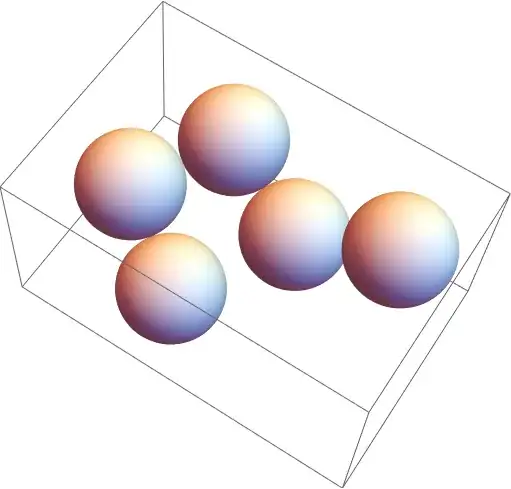
Sphere[], since it can support multiple centers if the radius is fixed:Graphics3D[Sphere[NestList[With[{rp = RandomPoint[Sphere[#, 1]]}, 2 rp - #] &, {0, 0, 0}, 5], 1]]– J. M.'s missing motivation Aug 05 '20 at 14:55