0

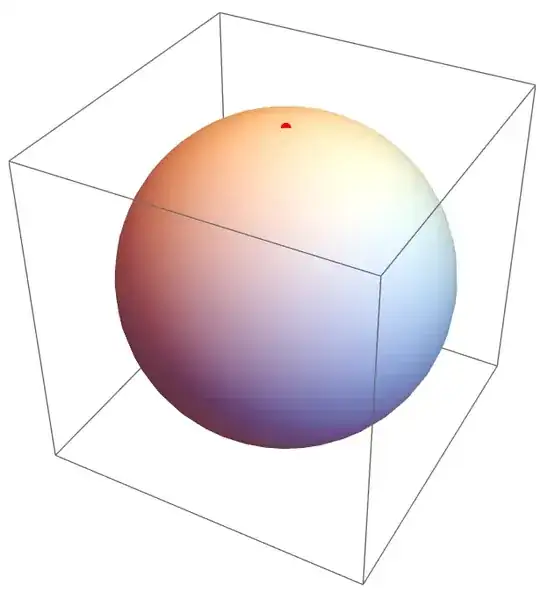
Suppose I have a unit Sphere[] sitting at the center {0,0,0}, with a point on its "north pole", like this one:

myUnitSphere = Sphere[{0,0,0}];
myUpperPoint = {0, 0, 1};

Graphics3D[{myUnitSphere, Red, PointSize[0.02], Point[myUpperPoint]}]

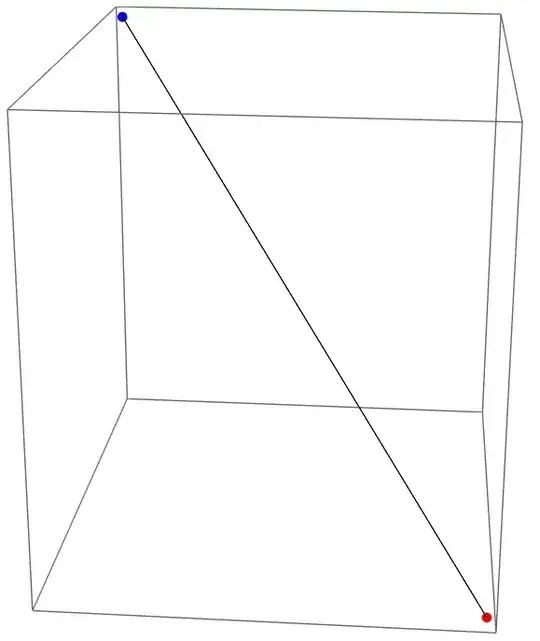
enter image description here

Now, suppose I have two arbitrary points in 3D forming a line:

myArbitraryPoints={{0.540689, 0.178886, -0.636606}, {-0.0768862, 0.911883, 0.0489186}};

Graphics3D[{Line[myArbitraryPoints], Red, PointSize[0.02], Point[myArbitraryPoints[[1]]], 
  Blue, PointSize[0.02], Point[myArbitraryPoints[[2]]]}]

enter image description here

How could I reorient both mySphere & myUpperPoint so that they are "aligned" to the axis (the line) formed by myArbitraryPoints?

How could this reorientation be done so that the red point on the sphere is reoriented with either the red point of the line or with the blue point? How could this be done so that the original center of the sphere does not change (currently at {0,0,0})? An ideal solution would accept points sitting on arbitrary locations (i.e. not only the pole), and also would work for more than one point on the sphere (like in this question), although in this case, one could choose one "reference point" to reorient all of them together with the sphere (maybe there's a simpler solution in this case, though).

Thanks!

TumbiSapichu
  • 1,603
  • 8
  • 17
  • http://reference.wolfram.com/language/ref/RotationTransform.html : RotationTransform[{u,v}] gives a rotation about the origin that transforms the vector u to the direction of the vector v. – flinty Jul 15 '20 at 00:32
  • Thanks! Pardon my ignorance, but what type of input should I feed into RotationTransform[{u,v}]? I did read the documentation of this, but my geometry knowledge is quite limited to say the least. I tried RotationTransform[{myUnitSphere, myArbitraryPoints}] but I don't get any result, and also I'd like to rotate both the sphere and its point(s). Should the point be rotated with RotationTransform[{u, v}, p] instead? Thanks! – TumbiSapichu Jul 15 '20 at 00:38
  • 1
    If you want a sphere centered at {0,0,0} and aligned so that {0,0,0}->myUpperPoint is parallel to the line then do alignvec = myArbitraryPoints[[2]] - myArbitraryPoints[[1]] to get the vector. Then get the transform with transform = RotationTransform[{myUpperPoint, alignvec}]. Then apply the transform to the sphere with transform@myUnitSphere. It's easier to see if you texture the sphere as well. – flinty Jul 15 '20 at 00:41

0 Answers0