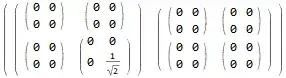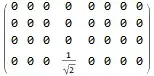How to rewrite a tensor as a matrix

Question

I put
{TensorProduct[{1, 0}, {0, 1}, {0, 1}, {0, 1}, {0, 1}]}/Sqrt[2]//MatrixForm and I got $$ \left( \begin{array}{cc} \left( \begin{array}{cc} \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right) & \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right) \\ \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right) & \left( \begin{array}{cc} 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} \\ \end{array} \right) \\ \end{array} \right) & \left( \begin{array}{cc} \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right) & \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right) \\ \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right) & \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right) \\ \end{array} \right) \\ \end{array} \right) $$ as a result. I now would like to rewrite this as $$ \left( \begin{array}{cc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{1}{\sqrt{2}} & 0 & 0 & 0 & 0 \end{array} \right) $$ to calculate eigenvalues of this matrix above.

Could you tell me how?

score 10 · Answer 1 · answered Jul 17 '20 at 18:50

mat = {TensorProduct[{1, 0}, {0, 1}, {0, 1}, {0, 1}, {0, 1}]/Sqrt[2]};

FixedPoint[ArrayFlatten, mat] // MatrixForm

$\left( \begin{array}{cccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{\sqrt{2}} & 0 & 0 & 0 & 0 \\ \end{array} \right)$

OkkesDulgerci · Answer 2 · 2020-07-18T03:09:02.000

8

mat = {TensorProduct[{1, 0}, {0, 1}, {0, 1}, {0, 1}, {0, 1}]/ Sqrt[2]};

ArrayFlatten[ArrayFlatten /@ mat] // MatrixForm

$\left( \begin{array}{cccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{\sqrt{2}} & 0 & 0 & 0 & 0 \\ \end{array} \right)$

edited Jul 18 '20 at 03:09

answered Jul 17 '20 at 14:00

OkkesDulgerci

10,716
1
19
38

1

Yes, it was a typo. Thanks for catching.. – OkkesDulgerci Jul 18 '20 at 03:09

score 7 · Answer 3 · answered Jul 17 '20 at 11:46

7

X = {TensorProduct[{1, 0}, {0, 1}, {0, 1}, {0, 1}, {0, 1}]/Sqrt[2]};

Flatten[X, {{1, 3, 5}, {2, 4, 6}}]

(*    {{0, 0, 0, 0, 0, 0, 0, 0},
       {0, 0, 0, 0, 0, 0, 0, 0},
       {0, 0, 0, 0, 0, 0, 0, 0},
       {0, 0, 0, 1/Sqrt[2], 0, 0, 0, 0}}    *)

answered Jul 17 '20 at 11:46

Roman

47,322
2
55
121

2

Side note: to understand this syntax of Flatten, one may read this answer. – xzczd Jul 17 '20 at 12:12

score 5 · Answer 4 · answered Jul 17 '20 at 11:25

5

Another option

(m = {TensorProduct[{1, 0}, {0, 1}, {0, 1}, {0, 1}, {0, 1}]}/Sqrt[2]) // MatrixForm

Mathematica graphics

And now

m1 = ArrayFlatten[m[[1, 1]], 2]
m2 = ArrayFlatten[m[[1, 2]], 2]
Join[m1, m2, 2] // MatrixForm

Mathematica graphics

answered Jul 17 '20 at 11:25

Nasser

143,286
11
154
359

How to rewrite a tensor as a matrix

4 Answers4