There are several problems if to attempt to solve this question with the ordinary methods like FindShortestTour.
Mathematica traditionally annoys first time users with the travelling salesman alike problems. Many authors have therefore published in their introductory books handwritten and so specially adopted and adaptable routine to solve this for their handsome readers. But this is a hard problem for professional measures.
So in literature, it is unusual to use the Mathematica built-in graph data structure and even the edge list and the edge list are seldom. The reason is evident. It is like in this question possible to deviate some the so intrinsic euclidian measure of the real world. That is already indicted in the copied picture the problem is not treatable with a metric like Manhattan distance and else.
The situation looks like this

The problem might be solved in manners like that in house-of-santa-claus.
That problem has not weights and the solution is so general in the node, knots it can not be transfered to this question directly.
listpoints = {{0, 0}, {177.9189, 125.972}, {410, 0}, {503.140,
83.366}}
Since this is mathematics there is a trick!
I suggest the code from Comparing Algorithms For The Traveling Salesman Problem. There is the need for the exact position for the last node, knot.
And there comes somehow the flaw of the design of the question into range. Only the 75 weight is in need to be satisfied. The 440 can be shortened to fit.
So another path is divide into loops and solve for the loops.
Sort[410, 510, 218, 218, 75, 329, 75, 440, 440, 329, 510,
125, 125, 410]
{75,125,218,329,440,510}
Anneal the weights and discard 440 and 510. Travel along the other egdes covers the graph. This is the main drawback of all Mathematica built-ins for such questions. They cover the graph and use all edges and all knots. That is not needed in general for traveling salesman problems.
Home -> Postoffice -> Bookshop -> Postoffice -> Supermarket -> Home is the minimal length in weight path. No other covers the reach of all nodes/knots.
The last step needs extra effort because the edge Supermarket -> Home can not be considered for the annealing with Mathematica built-ins
gred = Graph[{1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 3,
3 \[UndirectedEdge] 2, 3 \[UndirectedEdge] 4,
4 \[UndirectedEdge] 2}, EdgeWeight -> {218, 510, 329, 440, 75},
VertexLabels -> "Name", EdgeLabels -> "EdgeWeight",
VertexCoordinates -> {1 -> {0, 0}, 2 -> {0.2, 1}, 3 -> {1.2, 0.8},
4 -> {0.4, 1.7}}]
FindPostmanTour[gred] // First
{1 [UndirectedEdge] 3, 3 [UndirectedEdge] 4, 4 [UndirectedEdge] 2,
2 [UndirectedEdge] 3, 3 [UndirectedEdge] 2, 2 [UndirectedEdge] 1}
Seems Mathematica uses the loop partioning first and than adds up.
gred = Graph[{1 \[UndirectedEdge] 2, 3 \[UndirectedEdge] 2,
4 \[UndirectedEdge] 2}, EdgeWeight -> {218, 329, 75},
VertexLabels -> "Name", EdgeLabels -> "EdgeWeight",
VertexCoordinates -> {1 -> {0, 0}, 2 -> {0.2, 1}, 3 -> {1.2, 0.8},
4 -> {0.4, 1.7}}]
FindPostmanTour[gred] // First
{1 [UndirectedEdge] 2, 2 [UndirectedEdge] 4, 4 [UndirectedEdge] 2,
2 [UndirectedEdge] 3, 3 [UndirectedEdge] 2, 2 [UndirectedEdge] 1}
Replace the two edges then:
{1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 4, 4 \[UndirectedEdge] 2,
2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 1}
Chance has to replace the undirected egdes in this one case into a directed one from 3 to 1 first and than use Mathematica built-ins or solutions from other authors.
There is a difference between tsp with little nodes/knots and larger ones. They are usually treated different. For small numbers of knots it is cheaper to think first and than use Mathematica built-ins than other way round.
The detour, longer path than in real-world present makes this problem special.
The question of whether all edges and nodes shall be used is intrinsic to Mathematical built-ins. It saves a lot of programming to anneal first. Most tsp problems allow ordering and annealing. That is the comfortable perspective of such kind of problems.

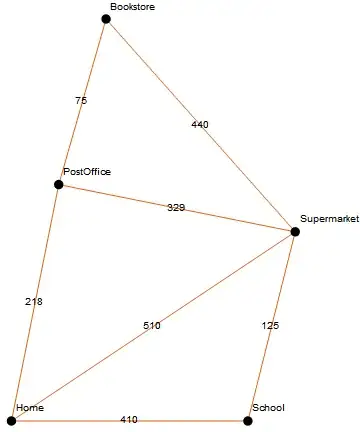


FindShortestTour[g]? You'll need to delete the duplicate edges and corresponding weights to get it to work, for example you have bothHome \[UndirectedEdge] SchoolandSchool \[UndirectedEdge] Homebut you only need one edge. – flinty Jul 25 '20 at 01:22FindShortestTour[SimpleGraph[g]]which will prune the extra edges and find the shortest tour.{2536, {Home, School, Supermarket, Bookstore, PostOffice, Home}}If you don't care about the school in the question, just remove it from the graphFindShortestTour[VertexDelete[SimpleGraph[g], School]]gives{2486, {Home, PostOffice, Bookstore, Supermarket, Home}}This is okay, because even though the School provides access on the home-supermarket route, it's cost is higher (410+125) than the direct route (510) – flinty Jul 25 '20 at 01:31someoneto walk through some nodes repeatedly, but I didn't know how to do it. – A little mouse on the pampas Jul 25 '20 at 01:51