3

I've been asked to factor the following polynomial:

poly = 6 x^3 + x^2 y - 11 xy^2 - 6 y^3 - 5 x^2 z + 11 xyz + 11 y^2 z - 2 xz^2 - 6 yz^2 + z^3

And to solve for z so that poly = 0

Can anyone help me with the syntax for factoring polynomials with unlike terms in Mathematica?

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
deathonater
  • 31
  • 1
  • Here is the answer : http://mathematica.stackexchange.com/questions/8255/factoring-polynomials-to-factors-involving-complex-coefficients It's neither too localized nor not a real question, but a duplicate. – Artes Apr 06 '13 at 18:17
  • It's not the same, really. The link is about 1D polys with complex-valued roots. This is about multi-D polys, and the second part of the question, about finding the null space does not occur in 1D. – bill s Apr 06 '13 at 19:08
  • There is always direct recourse to Solve. `In[3]:= Solve[poly == 0, z]

    Out[3]= {{z -> x + y}, {z -> 3 x + 2 y}, {z -> -2 x + 3 y}}`

     – Daniel Lichtblau Apr 06 '13 at 19:30

1 Answers1

3
poly = 6 x^3 + x^2 y - 11 x y^2 - 6 y^3 - 5 x^2 z + 11 x y z + 11 y^2 z - 2 x z^2 - 
       6 y z^2 + z^3;
Factor[poly]
sol = Solve[poly == 0, z]

d = Directive[Opacity[.7], Specularity[White, 60]];
Plot3D[z /. sol, {x, -1, 1}, {y, -1, 1}, Mesh -> None, 
      PlotStyle -> {{d, Red}, {d, Green}, {d, Blue}}, Evaluated -> True]

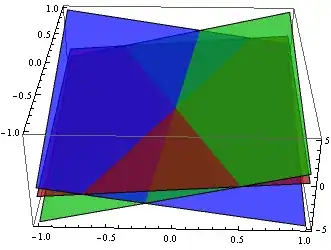
enter image description here

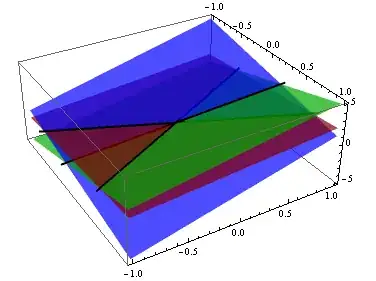
And

lins = Flatten[{x, y, t} /. Solve[#, {x, y}] & /@ 
                Thread /@ Thread[z == (z /. Subsets[sol, {2}])] /. z -> t, 1];
Show[Plot3D[z /. sol, {x, -1, 1}, {y, -1, 1}, Mesh -> None, 
            PlotStyle -> {{d, Red}, {d, Green}, {d, Blue}}, 
            Evaluated -> True,  BoundaryStyle -> None], 
     ParametricPlot3D[lins, {t, -10, 10}, PlotStyle -> Thick]]

Mathematica graphics

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453