Solve and Reduce fail here with rational parameter l, but succeed when I plug in a value
Assuming[ l ∈ Rationals && l > 0,
Solve[x Exp[-2/(x)] == (x - 1) - 1 /(2 l), x, Reals]]
% /. l -> 15/31
{{x -> 122/(60 + 61 ProductLog[-1, -60/(61 E^(60/61))])}}
Can I coax her to produce an answer which depends on the parameter? It turns out the equation can be solved by a series of substitutions, yielding $$x=\frac{d}{f + W_L(- f e^{-f})},\; d= 7- 2 l,\; f= \frac{2d\;l}{2 l+1}$$
It should be possible to convince Mathematica do release me from this chore :)
Edit two hours later:) Thanks for previous answers, but I'm still missing something. I found from papers like this one that I can reduce my equation to a canonic form
eq = (z - f) Exp[z] == -f
It is now a trivial case which can be solved by substitution $z-f=y$, but I want Mathematica to do all work.
Solve[eq, z, Method -> Reduce]
Solve[eq && z != 0, z, Method -> Reduce]
Solve[eq && z != 0 && z ∈ Reals, z, Method -> Reduce]
Solve[eq && z != 0 && z ∈ Reals && f ∈ Reals, z,
Method -> Reduce]
Solve[eq && z != 0, z, Method -> Reduce] /. C[1] -> 0
First Solve gets all cases; second removes some, but I still have the branch chooser C[1]. third time I say I want real roots, and I am reminded that f maybe complex. forth time I get an error
Solve::nsmet: This system cannot be solved with the methods available to Solve.
So, fifth time I give up, erase the two last assumptions, and decide to "talk simple" to Mathematica with C[1] -> 0 OK...
Still, it is a pity that f ∈ Reals did not succed, like it does
when I choose f from the start
Solve[(eq /. f -> 5/2) && z != 0 && z ∈ Reals, z, Method -> Reduce]

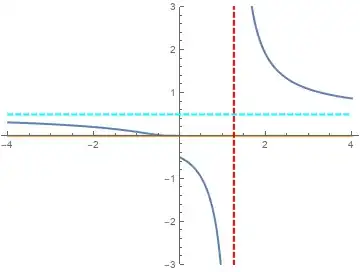


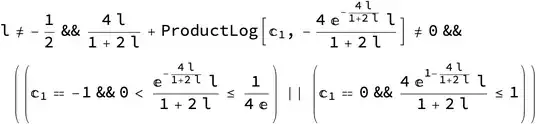

x == 2/((4 l)/(2 l + 1) + ProductLog[-1, -((4 l)/(1 + 2 l)) E^(-((4 l)/(1 + 2 l)))])but I cannot coax Mathematica to yield it either. – Roman Aug 12 '20 at 09:37Solvedoes not use the optionAssumptions. The assumptions should be included in theSolveas constraints. In cases whereSolveproduces a result (which it does not here), includingSimplifyorFullSimplifyin theAssumingwould then make use of the assumptions. – Bob Hanlon Aug 12 '20 at 12:20