6

Bug introduced in 12.1.1 and persisting through 13.2.0.

In the course of answering question 228693, I found that

ParametricNDSolveValue[{D[z[u, v], u, v] + z[u, v] == 0, z[u, -1] == Cos[1/2 (-1 + u) ω],
    z[1, v] == Cos[1/2 (1 + v) ω]}, z, {u, 1, 2}, {v, -2, -1}, {ω}]
%[1]

produces what appears to be to be a valid ParametricFunction but then causes the kernel to crash. (Incidentally, replacing z[u, -1] == Cos[1/2 (-1 + u) ω] by z[u, -1] == 1 and z[1, v] == Cos[1/2 (1 + v) ω] by z[1, v] == 1 eliminates the problem.) In contrast,

NDSolveValue[{D[z[u, v], u, v] + z[u, v] == 0, z[u, -1] == Cos[1/2 (-1 + u) ω], 
    z[1, v] == Cos[1/2 (1 + v) ω]} /. ω -> 1, z, {u, 1, 2}, {v, -2, -1}]

is well behaved. Is this a bug, or am I missing something obvious? I am using

$Version
(* "12.1.1 for Microsoft Windows (64-bit) (June 19, 2020)" *)

Some additional observations:

Several comments below plus my own more recent observations may be worth considering.

  1. Ulrich Neumann pointed out, and I have confirmed, that adding Method-> "FiniteElement" allows the first block of code above to produce a solution. Unfortunately, the solution is incorrect. For completeness, the solution I believe to be correct is below.
  2. Bob Hanlon pointed out, and I have confirmed, that adding WorkingPrecison with most any numerical value, including $MachingPrecison, causes the second block of code above to fail.
  3. The notebook I first used to demonstrate the kernel crash no longer causes that crash. However, copying the first block of code from the question to a new notebook and running it again produces the crash. More generally, I now have observed that the crash, although typical, is not always reproducible.
  4. When I monitored the notebook with the first block of code by means of Microsoft Task Manager, sometimes Mathematica hangs, sometimes not.

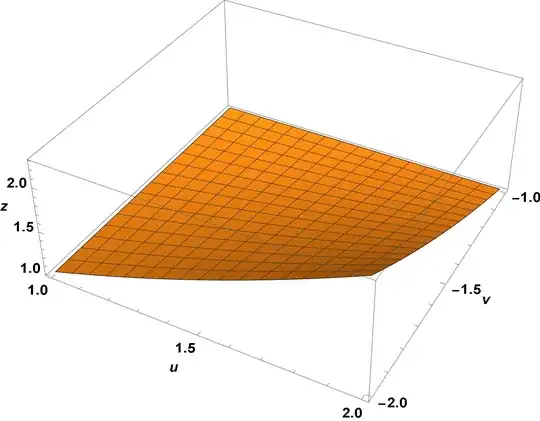
enter image description here

user21
  • 39,710
  • 8
  • 110
  • 167
bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
  • 1
    Even the case z[u,-1] == 1 causes the kernel crash for me and I have exactly same setup as you with Windows 10 (and I restarted MMA clean on each try). – Moo Aug 20 '20 at 14:47
  • 3
    Method-> "FiniteElement" gives a stable but somewhat strange parametric solution. – Ulrich Neumann Aug 20 '20 at 14:56
  • 1
    @Moo Thanks for catching my error, now corrected. – bbgodfrey Aug 20 '20 at 14:59
  • @UlrichNeumann I just plotted the solution with Method-> "FiniteElement". It looks very unstable. – bbgodfrey Aug 20 '20 at 15:32
  • @bbgodfrey Yes, not very smooth, but satisfies the boundary conditions ! – Ulrich Neumann Aug 20 '20 at 15:39
  • @UlrichNeumann So does the NDSolveValue result from my question, but the plot is smooth. – bbgodfrey Aug 20 '20 at 16:21
  • With v12.1.1 on a Mac and using NDSolveValue, when I attempt to set the WorkingPrecision I get one or more errors. The specific errors vary depending on the WorkingPrecision specified. – Bob Hanlon Aug 20 '20 at 19:11
  • @BobHanlon I get NDSolveValue::initf with the message, "The initialization of the method NDSolve StateSpace failed" in all cases, when I specify WorkingPrecision. Incidentally, it is easy to guess analytic solutions to the PDE, but DSolve does not return any. – bbgodfrey Aug 20 '20 at 19:40
  • The crash has been reported. – Daniel Lichtblau Aug 20 '20 at 22:29
  • 1
    Thanks, @DanielLichtblau. There are even more problems here. Using Method-> "FiniteElement" eliminates the crash but produces a nonsense answer. The notebook from which I produced the question now no longer exhibits the crash, but a new notebook with the code does. When I monitor the notebook with Microsoft Task Manager, sometimes Mathematica hangs, sometimes not. And, setting WorkingPrecision to any value causes NDSolveValue applied to the PDE generate an initialization error. This PDE seems cursed. – bbgodfrey Aug 20 '20 at 22:40

0 Answers0