BarLegend ticks distorted in MatrixPlot

Question

As shown in many threads here (this, this, ...), Ticks is a valid option of BarLegend. But it doesn't seem to work well in this simple MatrixPlot. Some ticks are just missing and 0.5 is obviously not at its right place (color). Note that I want the default plot with custom ticks. What am I missing here or any workaround?

data = Table[Sin[x] Cos[y], {x, 0, 2 Pi, 0.01}, {y, 0, 2 Pi, 0.01}];
MatrixPlot[data, 
 PlotLegends -> BarLegend[Automatic, "Ticks" -> {-0.5, 0, 0.5}], 
 LabelStyle -> Large]

Update:

a more general case with asymmetric data range

data = Table[Sin[x] Cos[y] + 0.05 x y, {x, 0, 2 Pi, 0.01}, {y, 0, 2 Pi, 0.01}]; 
MatrixPlot[data, PlotLegends -> BarLegend[Automatic, "Ticks" -> {-0.2, 0.5, 1.1}], 
LabelStyle -> Large]

kglr · Accepted Answer · 2020-09-06T10:14:18.090

Update: The function Graphics`ArrayPlotDump`Private`HybridRankingAndNaturalScale performs the mysterious "scaling based on a mixture of relative value and ranking for each matrix element". We construct a piecewise re-scaling function (reScale) using mpReScale and use it to specify the option value for "Ticks":

ClearAll[reScale,  cfMinMax]
reScale[{min_, max_}, {cfmin_, cfmax_}]  := 
  If[# < 0, Rescale[#, {min, 0}, {cfmin, 1/2}], Rescale[#, {0, max}, {1/2, cfmax}]] &;
cfMinMax = MinMax @ GraphicsArrayPlotDumpPrivate`HybridRankingAndNaturalScale[
   Union @ SparseArray[#]["NonzeroValues"], 0., {0, 1}, .5] &;

Examples:

data = {{1, 2, 1}, {2, 0, 1}, {0, -5, -1}};
ticks = {-4, -2, 3/2, 2};
cfminmax = cfMinMax[data];
minmax = MinMax @ data;
Row[{MatrixPlot[data, ImageSize -> 400, 
   PlotLegends -> BarLegend[Automatic], LabelStyle -> 16, 
   PlotLabel -> "default"], 
  MatrixPlot[data, ImageSize -> 400, 
   PlotLegends -> BarLegend[Automatic, 
     "Ticks" -> (Transpose[{reScale[minmax, cfminmax] /@ #, #}] & @ ticks)], 
   LabelStyle -> 16, 
   PlotLabel -> Row[{"Ticks : ", ticks}]]}, Spacer[10]]

An aside: We can use another undocumented option to specify tick labels

BarLegend[Automatic, "TickLabels" -> ticks, 
    "Ticks" -> (reScale[minmax, cfminmax] /@ ticks)]

to get the picture in the second plot above.

Change data and ticks to

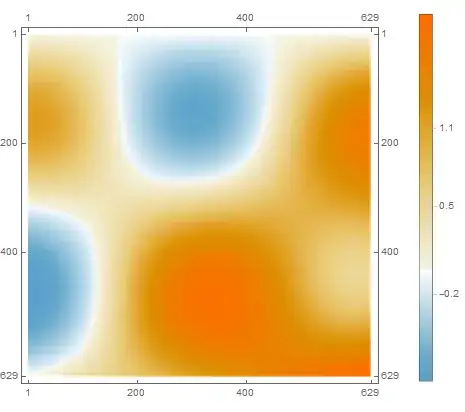
data = Table[Sin[x] Cos[y], {x, 0, 2 Pi, 0.01}, {y, 0, 2 Pi, 0.01}];
ticks = {-0.5, 0, 0.5};

to get

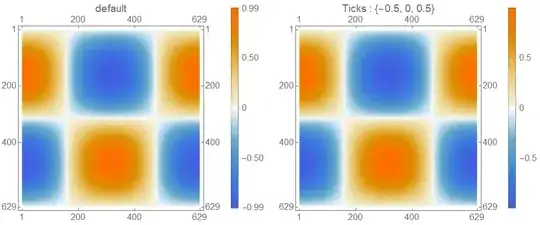
Using the second example in OP:

data = Table[Sin[x] Cos[y] + 0.05 x y, {x, 0, 2 Pi, 0.01}, {y, 0, 2 Pi, 0.01}];
ticks = {-0.2, 0.5, 1.1};

we get

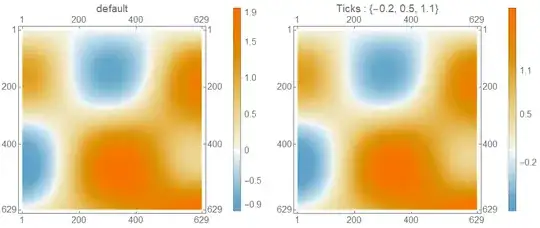
With

data = 1. + Table[Sin[x] Cos[y] + 0.05 x y, {x, 0, 2 Pi, 0.01}, {y, 0, 2 Pi,  0.01}] ;
ticks = {0.1, 0.5, 1.1, 2};

we get

Original answer:

This seems to be related to the special way scaling is done in MatrixPlot as mentioned in MatrixPlot >> Details and Options

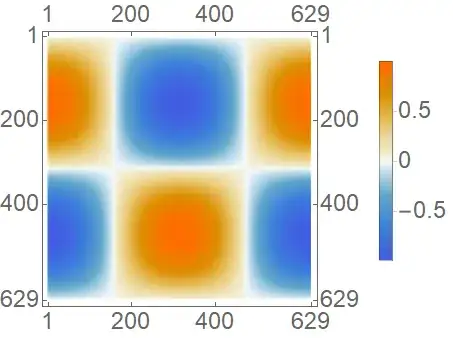
Easiest fix is in OP's case is to change the tick specification to Transpose[{Rescale[#, {-1, 1}, {0, 1}], #} &@{-0.5, 0, 0.5}]:

MatrixPlot[data, 
 PlotLegends -> 
  BarLegend[Automatic, 
   "Ticks" -> Transpose[{Rescale[#, {-1, 1}, {0, 1}], #} & @ {-0.5, 0, 0.5}]], 
 LabelStyle -> Large]

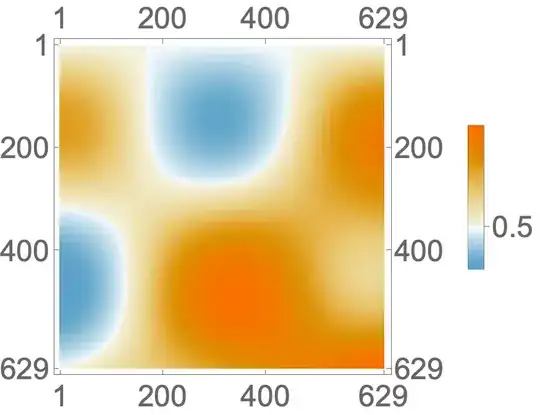
As an alternative (more general) work-around use the default color function with re-scaled argument and the option ColorFunctionScaling -> False:

defaultCF = "DefaultColorFunction" /.
    (Method /. Charting`ResolvePlotTheme[Automatic, MatrixPlot])

 Blend[System`PlotThemeDump`$ThemeDefaultMatrix, #1] &

MatrixPlot[data, 
 ColorFunction -> (defaultCF[Rescale[#, {-1, 1}]] &), 
 ColorFunctionScaling -> False, 
 PlotLegends -> BarLegend[Automatic, "Ticks" -> {-0.5, 0, 0.5}], 
 LabelStyle -> Large]

Alternatively, specify the color function in BarLegend:

MatrixPlot[data, 
 PlotLegends -> BarLegend[{defaultCF[Rescale[#, {-1, 1}]] &, {-1, 1}}, 
   ColorFunctionScaling -> False, "Ticks" -> {-0.5, 0, 0.5}], 
 LabelStyle -> Large]

Thank you for the nice explanation! But how about a more general case updated in the question? Your first method doesn't work well. Your second method (if I change {-1,1} to MinMax@data) produces something rather different from the default plot (maybe zero shifted?). Can I still get the default plot with the tick problem fixed? — xiaohuamao, Sep 04 '20 at 16:56
Another issue with your second method is the following. Say we have data1=data and another different data2 (MWE is just data2=data+1.0). We then make plot1 plot2 and combine as Grid[{{plot1, plot2}}]. Then the first BarLegend color is distorted. In any case, to obtain the default plot is probably the first thing. Thank you! — xiaohuamao, Sep 04 '20 at 18:29
Hello. I'm sorry that I still find serious flaws. Let's say we use the second data in the question and ticks = {-0.9, 0.5, 1.1}, then -0.9 is missing in Method 1. Although -0.9 is not missing in Method 2/3, the big problem is Method 2/3 in general can give very different plot from the original/Method 1. This is not obvious in the current data, but very obvious in data+1.0 for instance. Could you please help with this? Thanks! — xiaohuamao, Sep 06 '20 at 01:10
Another example of missing ticks would be the aforementioned data+1.0 with ticks={0.5,1.1,2} where 2 is lost and one can see by eyes that the positions of 0.5 and 1.1 do not match the original BarLegend scale. The current rescale method seems not capturing the default scale well. — xiaohuamao, Sep 06 '20 at 01:53
Thank you for the update. This looks to work for the second data in the post but not for data+1.0 mentioned above, which is basically newdata = Table[ Sin[x] Cos[y] + 0.05 x y + 1, {x, 0, 2 Pi, 0.01}, {y, 0, 2 Pi, 0.01}] with ticks = {0.1, 0.5, 1.1, 2}. Method 1 loses track of ticks while Method 2 cannot plot normally. — xiaohuamao, Sep 06 '20 at 08:14
@xiaohuamao, gave up on the second and third methods. Hope the new version of the first method works for all your cases. — kglr, Sep 06 '20 at 09:24
Thank you so much for your continual help! This now seems to work well as far as I've tried. Now we explicitly make use of the built-in Graphics`ArrayPlotDump`Private`HybridRankingAndNaturalScale for MatrixPlot. Although I'm not sure whether uniform scaling respectively on the positive and negative axis is the built-in scaling, at least piecewise for positive and negative is true. So I feel it is quite plausible and may be the same as the built-in one. — xiaohuamao, Sep 06 '20 at 18:51
@xiaohuamao LinearModelFit suggests it's indeed uniform scaling. See my answer for more info. — xzczd, Sep 07 '20 at 08:43

score 3 · Answer 2 · answered Sep 07 '20 at 08:38

kglr has already resolved the problem, here's just some additional analysis and another possible work-around.

First of all, I don't think this is a bug, becauce by default MatrixPlot knows how to set proper Ticks for BarLegend:

plot = MatrixPlot[data, ImageSize -> 400, PlotLegends -> Automatic]

Looking into the plot, we find that:

plot[[2, 1]] // InputForm
(*
BarLegend[{Blend[System`PlotThemeDump`$ThemeDefaultMatrix, #1] & , 
  {0.2889327547713697, 1.}}, LabelStyle -> {}, 
 LegendLayout -> "Column", LegendMarkerSize -> 400, 
 Ticks -> {{0.39446607623278385, -0.5}, {0.5, 0.}, {0.3100389372190109, 
  -0.9}, {0.626985112913238, 0.5}, {0.753970225826476, 1.}, 
  {0.880955338739714, 1.5}, {0.9825434290703043, 1.9000000000000001}}, 
 "PinningPoint" -> 0.5, "SmoothRange" -> False, 
 Charting`TickSide -> Right, ColorFunctionScaling -> False]
 *)

As we can see, the ticks of BarLegend are set by the undocumented Ticks option, we plot the ticks:

autotick = Cases[plot[[2, 1]], (Ticks -> a_) :> a][[1]] // Sort
ListLinePlot[autotick]

Not hard to notice it's a piecewise line, splitting at {0.5, 0.}. We can further verify this with LinearModelFit:

LinearModelFit[autotick[[#]], {1, x}, x]["RSquared"] & /@ {;; 3, 3 ;;}
(* {1., 1.} *)

So, even if we're not aware of the Graphics`ArrayPlotDump`Private`HybridRankingAndNaturalScale, we can still rescale the ticks in the following manner:

ticks = {-0.2, 0.5, 1.1}
Clear[rescale]
rescale[tick_List, rest__] := rescale[#, rest] & /@ tick
rescale[tick_?Positive, mysteryminmax_, {min_, max_}] := 
 Rescale[tick, {0, max}, {1/2, mysteryminmax[[2]]}]
rescale[tick_, mysteryminmax_, {min_, max_}] := 
 Rescale[tick, {min, 0}, {mysteryminmax[[1]], 1/2}]
plot /. (Ticks -> _) :> (Ticks -> {rescale[ticks, 
       Sequence @@ (autotick[[{1, -1}]][Transpose])], ticks}[Transpose])

Thank you! It further clarifies the problem. – xiaohuamao Sep 07 '20 at 16:35 — xiaohuamao, Sep 07 '20 at 16:35

BarLegend ticks distorted in MatrixPlot

Update:

2 Answers2

Linked