I want to write a custom function that outputs the Taylor series as follows:
$$f(X)=f\left(X^{(0)}\right)+\nabla f\left(X^{(0)}\right)^{T} \Delta X+\frac{1}{2} \Delta X^{T} G\left(X^{(0)}\right) \Delta X+\cdots $$
$$G\left(X^{(0)}\right)=\left.\left(\begin{array}{cc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} \end{array}\right)\right|_{X^{(0)}}, \Delta X=\left(\begin{array}{c} \Delta x_{1} \\ \Delta x_{2} \end{array}\right)$$
That is to say, what I need is the following format that keeps the matrix from being computed:
$$f(X)=f\left(X^{(0)}\right)+\left(\frac{\partial f}{\partial x_{1}}, \frac{\partial f}{\partial x_{2}}\right)_{X^{(0)}}\left(\begin{array}{c} \Delta x_{1} \\ \Delta x_{2} \end{array}\right)+\left.\frac{1}{2}\left(\begin{array}{ccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} \end{array}\right)\right|_{X^{(0)}}\left(\begin{array}{c} \Delta x_{1} \\ \Delta x_{2} \end{array}\right)+\cdots $$
(I need to keep the matrix $\left.\left(\begin{array}{cc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} \end{array}\right)\right|_{X^{(0)}}$ and vector $\left(\begin{array}{c} \Delta x_{1} \\ \Delta x_{2} \end{array}\right) $ in a non operational format).
The user-defined function should be universal and can be applied to the Taylor series of any n-variable function.
F[k_] := Sum[
Binomial[k, r]*Δx^r*Δy^(k - r)*
Derivative[r, k - r][f][x0, y0], {r, 0, k}]
Expand[Sum[F[i]/i!, {i, 0, 3}]]
grads = NestList[Grad[#1, {x1, x2, x3}] & , f[x1, x2, x3],
6] /. {x1 -> 0, x2 -> 0, x3 -> 0};
[DoubleStruckCapitalX] = {Δx1, Δx2,
Δx3};
Expand[(1/0!)grads[[1]] + (1/1!)
grads[[2]] . [DoubleStruckCapitalX] + (1/2!)*
grads[[3]] . [DoubleStruckCapitalX] . [DoubleStruckCapitalX] +
(1/3!)*
grads[[4]] . [DoubleStruckCapitalX] . [DoubleStruckCapitalX] .
[DoubleStruckCapitalX]]
However, the results of the above codes can not keep the matrix and vector format. What can I do to get the output format I want?
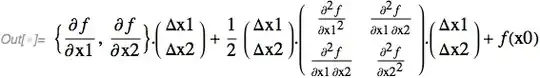
Inactivate[{1, 2, 3}.{4, 5, 6}]– chris Sep 05 '20 at 06:27