Cannot derive `Norm` or `Normalize` when recreating Frenet Serret equations

Question

I'm trying to calculate the torsion of a curve at a point using the following code:

r[t_] := {t, 0.1 t^2, 0.1 t^3}
T[t_] := Normalize[r'[t]]
n[t_] := Normalize[T'[t]]
B[t_] := Cross[T[t], n[t]]
Torsion[t_] := -1*Dot[n[t], D[B[t]]]/Norm[r'[t]] 
Plot[
 Torsion[t],
 {t, -5, 5}
 ]

N[Torsion[3.16]] gives:

-0.310482 (((0. - 0.182773/Sqrt[
      Abs[0.588674 - 0.520593 Derivative[1][Abs][3.16]]^2 + 
       Abs[0.0620965 - 0.10983 Derivative[1][Abs][3.16]]^2 + 
       0.0302 Abs[Derivative[1][Abs][3.16]]^2]) (0.0620965 - 
      0.10983 Derivative[1][Abs][3.16]))/Sqrt[
   Abs[0.588674 - 0.520593 Derivative[1][Abs][3.16]]^2 + 
    Abs[0.0620965 - 0.10983 Derivative[1][Abs][3.16]]^2 + 
    0.0302 Abs[Derivative[1][Abs][3.16]]^2] - (
   0.173781 (0. + 0.0577563/Sqrt[
      Abs[0.588674 - 0.520593 Derivative[1][Abs][3.16]]^2 + 
       Abs[0.0620965 - 0.10983 Derivative[1][Abs][3.16]]^2 + 
       0.0302 Abs[Derivative[1][Abs][3.16]]^2]) Derivative[1][Abs][
     3.16])/Sqrt[
   Abs[0.588674 - 0.520593 Derivative[1][Abs][3.16]]^2 + 
    Abs[0.0620965 - 0.10983 Derivative[1][Abs][3.16]]^2 + 
    0.0302 Abs[Derivative[1][Abs][3.16]]^2] + ((0.588674 - 
      0.520593 Derivative[1][Abs][3.16]) (0.0192799/Sqrt[
      Abs[0.588674 - 0.520593 Derivative[1][Abs][3.16]]^2 + 
       Abs[0.0620965 - 0.10983 Derivative[1][Abs][3.16]]^2 + 
       0.0302 Abs[Derivative[1][Abs][3.16]]^2] + (
      6.93889*10^-18 Derivative[1][Abs][3.16])/Sqrt[
      Abs[0.588674 - 0.520593 Derivative[1][Abs][3.16]]^2 + 
       Abs[0.0620965 - 0.10983 Derivative[1][Abs][3.16]]^2 + 
       0.0302 Abs[Derivative[1][Abs][3.16]]^2]))/Sqrt[
   Abs[0.588674 - 0.520593 Derivative[1][Abs][3.16]]^2 + 
    Abs[0.0620965 - 0.10983 Derivative[1][Abs][3.16]]^2 + 
    0.0302 Abs[Derivative[1][Abs][3.16]]^2])

It seems to be having a problem with deriving the absolute value function, but for a real-number, the derivative should exist. I tried using FullSimplify to no avail.

Replacing Norm and Normalize with:

Normalise[v_] := Norm1[v]* v
Norm1[v_] := Sqrt[Dot[v, v]]

will let the graph render, but it does not appear like the FrenetSerretSystem[r[t], t][[1]][[2]] graph, as it should.

These ResourceFunctions can make your life much easier https://resources.wolframcloud.com/FunctionRepository/search/?i=torsion and https://resources.wolframcloud.com/FunctionRepository/resources/CurveTorsion — flinty, Sep 06 '20 at 22:14
The example in the question is the same as I used here Finding unit tangent, normal, and binormal vectors for a given r(t) (instead of 0.1 I recommend using 1/10). Wouldn't it be simpler to copy this approach or this one? — Artes, Sep 06 '20 at 22:34
Yeah that would be easier, but the point of this is for me to learn how the FernetSerret System works, so I want to type in the equations from my textbook into Mathematica and manipulate them so I can test the book's claims. — swissnetizen, Sep 07 '20 at 07:53
Possible duplicate: https://mathematica.stackexchange.com/questions/8188/simplifying-the-derivative-of-x — Michael E2, Apr 17 '22 at 13:25

Daniel Huber · Accepted Answer · 2020-09-07T11:18:21.057

Consider: T[t]

{1/Sqrt[1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4], (0.2 t)/Sqrt[
 1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4], (0.3 t^2)/Sqrt[
 1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4]}

As you can see, it contains the function "Abs". In complex numbers, Abs is nowhere differentiable. And MMA assumes, without being told otherwise, that all numbers are complex. Because of this problem MMA introduces in version 11 the function RealAbs which is differentiable everywhere, except at the origin, where it arbitrarily set to 1. The same problem appears in the definition of n[t].

A further problem is the term D[B[t],t] in the definition of "Torsion[t]". If this is evaluated and t replaced by a number e.g. 1., we will have D[B1,1] what is nonsense. Therefore, you must write B'[t] for the derivative.

With this corrections:

r[t_] := {t, 0.1 t^2, 0.1 t^3}
T[t_] := Normalize[r'[t]] /. Abs -> RealAbs
n[t_] := Normalize[T'[t]] /. Abs -> RealAbs
B[t_] := Cross[T[t], n[t]]
Torsion[t_] := -1*Dot[n[t], B'[t]]/Norm[r'[t]]
Plot[Torsion[t], {t, -5, 5}]

Further may I point you to the function "FrenetSerretSystem" that gives curvature, torsion and the frenet system.

cvgmt · Answer 2 · 2020-09-08T07:38:10.437

2

According to Alfred Gray's Differential Geometry book,it is recommend to use the following way to calculate the torsion .

r[t_] := {t, 0.1 t^2, 0.1 t^3};
T[t_] := Normalize[r'[t]];
B[t_] := Normalize[Cross[r'[t], r''[t]]];
n[t_] := Cross[B[t], T[t]];
Torsion[t_] := 
 Det[{r'[t], r''[t], r'''[t]}]/Norm[Cross[r'[t], r''[t]]]^2
N[Torsion[3.16]]
(* 0.0300467 *)

edited Sep 08 '20 at 07:38

answered Sep 08 '20 at 07:09

cvgmt

72,231
4
75
133

score 0 · Answer 3 · answered Sep 08 '20 at 09:16

r[t_] := {t, 0.1 t^2, 0.1 t^3}
T[t_] := Normalize[r'[t]]
n[t_] := Normalize[T'[t]]

T[t]

({1/Sqrt[1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4], (0.2 t)/Sqrt[ 1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4], (0.3 t^2)/Sqrt[ 1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4]})

n[t]

({-((0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t])/(2 (1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^( 3/2) [Sqrt](1/ 4 Abs[(0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t])/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2 + Abs[0.2/Sqrt[1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4] - ( 0.1 t (0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t]))/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2 + Abs[(0.6 t)/Sqrt[1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4] - ( 0.15 t^2 (0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t]))/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2))), (0.2/Sqrt[ 1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4] - ( 0.1 t (0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t]))/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^( 3/2))/([Sqrt](1/ 4 Abs[(0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t])/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2 + Abs[0.2/Sqrt[1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4] - ( 0.1 t (0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t]))/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2 + Abs[(0.6 t)/Sqrt[1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4] - ( 0.15 t^2 (0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t]))/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2)), ((0.6 t)/Sqrt[ 1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4] - ( 0.15 t^2 (0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t]))/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^( 3/2))/([Sqrt](1/ 4 Abs[(0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t])/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2 + Abs[0.2/Sqrt[1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4] - ( 0.1 t (0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t]))/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2 + Abs[(0.6 t)/Sqrt[1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4] - ( 0.15 t^2 (0.08 Abs[t] Derivative[1][Abs][t] + 0.36 Abs[t]^3 Derivative[1][Abs][t]))/(1 + 0.04 Abs[t]^2 + 0.09 Abs[t]^4)^(3/2)]^2))})

That is where the problem is stemming from.

Have a look at Normalize. Even in the most common normalization, the Abs is used. As already stated, if nothing else is specified Mathematica works in the Complexes. So derivation of Abs is nowhere defined.

The derivation of T introduces the Abs again after the first Normalize did not introduce it in Mathematica V12.0.0.

The problem is not solved if the second argument is used with RealAbs.

So the path of the solution is

n[t_] := D[T[t], t]/Sqrt[D[T[t], t].D[T[t], t]]
n[t]

({-((0.08 t + 0.36 t RealAbs[t]^2)/(2 (1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^( 3/2) [Sqrt]((0.08 t + 0.36 t RealAbs[t]^2)^2/( 4 (1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^3) + (-(( 0.1 t (0.08 t + 0.36 t RealAbs[t]^2))/(1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^(3/2)) + 0.2/ Sqrt[1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4])^2 + (-(( 0.15 t^2 (0.08 t + 0.36 t RealAbs[t]^2))/(1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^(3/2)) + (0.6 t)/ Sqrt[1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4])^2))), (-(( 0.1 t (0.08 t + 0.36 t RealAbs[t]^2))/(1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^(3/2)) + 0.2/Sqrt[ 1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4])/([Sqrt]((0.08 t + 0.36 t RealAbs[t]^2)^2/( 4 (1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^3) + (-(( 0.1 t (0.08 t + 0.36 t RealAbs[t]^2))/(1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^(3/2)) + 0.2/Sqrt[ 1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4])^2 + (-(( 0.15 t^2 (0.08 t + 0.36 t RealAbs[t]^2))/(1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^(3/2)) + (0.6 t)/ Sqrt[1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4])^2)), (-(( 0.15 t^2 (0.08 t + 0.36 t RealAbs[t]^2))/(1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^(3/2)) + (0.6 t)/Sqrt[ 1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4])/([Sqrt]((0.08 t + 0.36 t RealAbs[t]^2)^2/( 4 (1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^3) + (-(( 0.1 t (0.08 t + 0.36 t RealAbs[t]^2))/(1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^(3/2)) + 0.2/Sqrt[ 1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4])^2 + (-(( 0.15 t^2 (0.08 t + 0.36 t RealAbs[t]^2))/(1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4)^(3/2)) + (0.6 t)/ Sqrt[1 + 0.04 RealAbs[t]^2 + 0.09 RealAbs[t]^4])^2))})

The rest is as usual and the best choice is FrenetSerretSystem.

FrenetSerretSystem[r[t], t]
{{Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4]/(1. + 0.04 t^2 + 0.09 t^4)^(3/2),
   33.3333/(
  11.1111 + 100. t^2 + 1. t^4)}, {{1./Sqrt[
   1. + 0.04 t^2 + 0.09 t^4], (0. + 0.2 t)/Sqrt[
   1. + 0.04 t^2 + 0.09 t^4], (0. + 0.3 t^2)/Sqrt[
   1. + 0.04 t^2 + 
    0.09 t^4]}, {-((0.04 t)/(
     Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[
      1. + 0.04 t^2 + 0.09 t^4])) - (0.18 t^3)/(
    Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[
     1. + 0.04 t^2 + 0.09 t^4]), 
   0.2/(Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[
     1. + 0.04 t^2 + 0.09 t^4]) - (0.018 t^4)/(
    Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[
     1. + 0.04 t^2 + 0.09 t^4]), (0.6 t)/(
    Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[
     1. + 0.04 t^2 + 0.09 t^4]) + (0.012 t^3)/(
    Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[
     1. + 0.04 t^2 + 0.09 t^4])}, {(0. + 0.06 t^2)/Sqrt[
   0.04 + 0.36 t^2 + 0.0036 t^4], -((0.6 t)/Sqrt[
    0.04 + 0.36 t^2 + 0.0036 t^4]), 0.2/Sqrt[
   0.04 + 0.36 t^2 + 0.0036 t^4]}}}

The answer to Your question is, that Normalize causes the problems because it checks the denominator for realness and positiveness after the squaring and summation is done. It replaces therefore each component square of the derivation of the normal with Abs. Abs is defined on the Complexes but can nowhere derivated on them so the derivation of the vector path has RealAbs and the derivation of the normal has Abs. That the way it is implemented in Mathematica.

That is not an error. There are two workarounds.

(1) give up the stability by using

r[t_] := {t, 0.1 t^2, 0.1 t^3}
T[t_] := Normalize[r'[t]]
n[t_] := D[T[t], t]/Sqrt[D[T[t], t].D[T[t], t]]

(2) by making use of FrenetSerretSystem[r[t], t]. See the details for FrenetSerretSystem on the Mathematica documentation page of FrenetSerretSystem. It is

curvature, torsion, tangent, normal, and binormal

In this question:

{"curvature"->{Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4]/(1. + 0.04 t^2 + 0.09 t^4)^(3/2)},
   "torsion"->{33.3333/(
  11.1111 + 100. t^2 + 1. t^4)},

{"tangent"->{1./Sqrt[ 1. + 0.04 t^2 + 0.09 t^4], (0. + 0.2 t)/Sqrt[ 1. + 0.04 t^2 + 0.09 t^4], (0. + 0.3 t^2)/Sqrt[ 1. + 0.04 t^2 + 0.09 t^4]},"normal"-> {-((0.04 t)/( Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[ 1. + 0.04 t^2 + 0.09 t^4])) - (0.18 t^3)/( Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[ 1. + 0.04 t^2 + 0.09 t^4]), 0.2/(Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[ 1. + 0.04 t^2 + 0.09 t^4]) - (0.018 t^4)/( Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[ 1. + 0.04 t^2 + 0.09 t^4]), (0.6 t)/( Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[ 1. + 0.04 t^2 + 0.09 t^4]) + (0.012 t^3)/( Sqrt[0.04 + 0.36 t^2 + 0.0036 t^4] Sqrt[ 1. + 0.04 t^2 + 0.09 t^4])},"binormal"-> {(0. + 0.06 t^2)/Sqrt[ 0.04 + 0.36 t^2 + 0.0036 t^4], -((0.6 t)/Sqrt[ 0.04 + 0.36 t^2 + 0.0036 t^4]), 0.2/Sqrt[ 0.04 + 0.36 t^2 + 0.0036 t^4]}}}

or as

basis = Last[FrenetSerretSystem[r[t], t]] // Simplify;
{tangent, normal, binormal} = Map[Arrow[{r[t], r[t] + #}] &, basis];

Manipulate[ Show[ParametricPlot3D[r[s], {s, 0, 2 Pi}, PlotStyle -> Thick], Graphics3D[{Thick, Blue, tangent, Red, normal, Purple, binormal}], PlotRange -> Full] // Evaluate, {t, 0, 2 Pi, Appearance -> {"Open"}}]

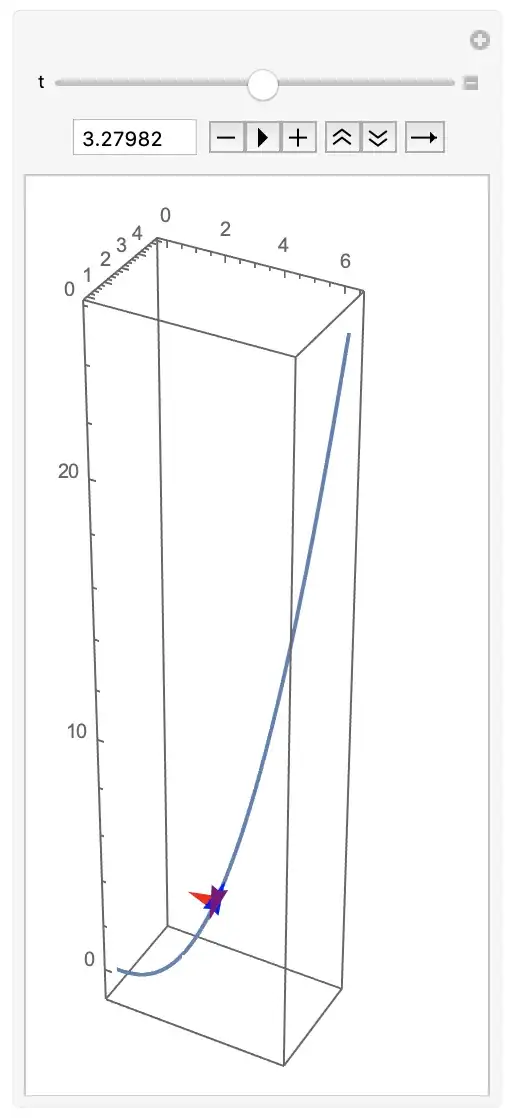
This solves the question is the necessary and professional depth.

Cannot derive `Norm` or `Normalize` when recreating Frenet Serret equations

3 Answers3

Linked