2

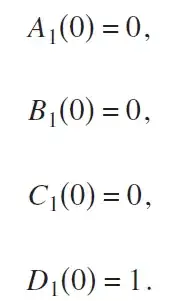
I'm getting trouble solving these 4 coupled differential equations, just can't get a result while it keep running. enter image description here

eqs = 
{
A1'[t] ==  I (μ0 - 2*g) A1[t] - I g0 (B1[t] + C1[t]), 
B1'[t] == -I (g0 (2 + n) A1[t] + Ω C1[t] + g0 D1[t]), 
C1'[t] == -I (g0 (2 + n) A1[t] + Ω B1[t] + g0 D1[t]), 
D1'[t] == -I g0 (1 + n) (B1[t] + C1[t]) - I (μ0 - 2 g) D1[t], 
A1[0] == 0, B1[0] == 0, C1[0] == 0, D1[0] == 1
};
dusol = DSolve[eqs, {A1, B1, C1, D1}, t][[1]] // FullSimplify
xzczd
  • 65,995
  • 9
  • 163
  • 468
karry
  • 381
  • 1
  • 9
  • Don't use \!\(\*SuperscriptBox[\(A1\), \('\)]\)[t] to describe the derivative. Use A1'[t] instead. – Ulrich Neumann Sep 16 '20 at 07:28
  • Good question. Something definitely is wrong! – bbgodfrey Sep 17 '20 at 00:15
  • Just to make sure, your trouble is DSolve runs forever, right? – xzczd Sep 17 '20 at 01:55
  • No, it reports error and can't run, let alone get a result. – karry Sep 17 '20 at 02:26
  • 1
    @xzczd The problem as stated runs forever for Version 12.1.1. Eliminating both the initial conditions and FullSimplify yields an enormous answer after several minutes. The matrix of the right sides of the equations is not Hermitian, but Eigensystem does produce results quickly. However, JordanDecomposition crashes. Possibly a bug. – bbgodfrey Sep 17 '20 at 02:28
  • Please edit your post to clarify the trouble you have. In v12.1.1 the code just just runs forever. Which version are you in? BTW, you need to add @xzczd in your comment, or I won't get the reminder. (You may want to read this post to learn the usage of @. ) – xzczd Sep 17 '20 at 02:32
  • @xzczd OK, I use the version 10.1. The error it outputs is "Syntax::sntxi: Incomplete expression; more input is needed." – karry Sep 17 '20 at 02:37
  • 1
    …You got this warning with \!\(\*SuperscriptBox[\(A1\), \('\)]\)[t], right? I guess you obtained this by stroking Ctrl + 6 first? Then you've typed ' in wrong way. You should directly type ' i.e. A1'[t] is the correct input. Now copy the code in your question back to Mathematica and retry. (BTW, if you insist on stroking Ctrl + 6 first, then what you should type is \[Prime]. ) – xzczd Sep 17 '20 at 02:43
  • @xzczd Yes, you are absolutely right! Now it just keep running . – karry Sep 17 '20 at 02:55
  • 1
    Problem with JordanDecomposition noted in earlier comment report to Wolfram, Inc as CASE:4633110. – bbgodfrey Sep 17 '20 at 13:50

1 Answers1

2

I've found 3 work-arounds.

First one is to make use of the ConstantsGrouping` package:

head = {A1, B1, C1, D1};
var = Through@head@t;

{newrhs, rule} = GroupConstants[eqs[[;; 4, -1]], {t, var} // Flatten]


lhs = eqs[[;; 4, 1]]


solmid = DSolve[{lhs == newrhs // Thread, eqs[[5 ;;]]}, head, t]; // AbsoluteTiming
(* {12.4674, Null} *)


sol = var /. solmid[[1]] /. rule;

Second one is based on LaplaceTransform:

teqs = LaplaceTransform[eqs[[;; 4]], t, s] /. Rule @@@ eqs[[5 ;;]]

tsol = Solve[teqs, LaplaceTransform[var, t, s]][[1, All, -1]]


sol2 = InverseLaplaceTransform[tsol, s, t]; // AbsoluteTiming
(* {0.968162, Null} *)

Last, and the fastest one is to utilize MatrixExp:

{barray, marray} = CoefficientArrays[eqs[[;; 4, -1]], var];

sol3 = MatrixExp[marray t, eqs[[5 ;;, -1]]]; // AbsoluteTiming
(* {0.458083, Null} *)
xzczd
  • 65,995
  • 9
  • 163
  • 468
  • Thank you very much for your solutions. They're very useful. I've solved my problem. And importantly, I left out the initial condition $μ0=2g,g0=g$! – karry Sep 19 '20 at 07:51