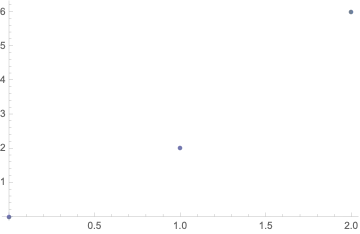
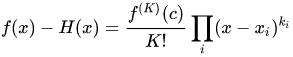How to calculate the expression of error truncation function?

Question

We already know that some node information of function f(x) is shown in the table below:

$$\begin{array}{|c|c|c|c|} \hline x_{i} & 0 & 1 & 2 \\ \hline f\left(x_{i}\right) & 0 & 2 & 6 \\ \hline f^{\prime}\left(x_{i}\right) & & 1 & \\ \hline \end{array}$$

Now I need to find the Hermite interpolation polynomial $H_{3}(x)$ of function f and give the expression of truncation error $R(x)=f(x)-H_{3}(x)$.

I have found the Hermite interpolation polynomial $H_{3}(x)$ by the following code:

InterpolatingPolynomial[{{0, 0}, {1, 2, 1}, {2, 6}}, x] // Expand

Or

(*https://mathematica.stackexchange.com/a/230256/42417*)
newton[{X_, Y_}, x_] := 
 Module[{f, asso = X -> Y // Thread // Association}, 
  f@{a_, b___, c_} := f@{a, b, c} = (f@{b, c} - f@{a, b})/(c - a);
  f@{a_} := asso@a;
  Sum[f@#*Times @@ (x - Most@#) &@X[[;; i]], {i, Length@X}]]
xx = {0., 1., 2.};
y = {0., 2., 6.};
H3 = newton[{xx, y}, x] + a (x - 0) (x - 1) (x - 2)
Solve[(D[H3, x] /. x -> 1) == 1, a]
H3 /. First[%] // Expand

But I don't know how to use MMA to find the expression of truncation error function $R(x)$. What should I do?

A post with a similar question

The reference answer is $R(x)=\frac{f^{4}(\xi )}{4 !} x(x-1)^{2}(x-2), \quad \xi \in[\min (0, x),\max (x, 2)]$:

Source of this problem$\color{Gray} {\text{(2008 武汉岩石数值分析 5)}} $:

We can refer to example 3 on page 103 of this book for similar questions.

@Moo $f(x)$ is an unknown differentiable function of at least fourth order. We know the value of its three nodes and the derivative of one node. Now we need to give its Hermite interpolation polynomial and truncation error expression. — A little mouse on the pampas, Sep 18 '20 at 03:00
Consider a concrete function, say $f(x):=\exp(x)$ to this end. — user64494, Sep 18 '20 at 07:51
Your reference answer is wrong, should be $R(x)=\frac{f^{4}(\xi )}{4 !} x(x-1)^{2}(x-2), \quad \xi \in [0,,2]$. — yarchik, Sep 26 '20 at 20:16
@yarchik Thank you for your comments, I have corrected the mistake. — A little mouse on the pampas, Sep 27 '20 at 01:18
For proper definitions consult [https://mathworld.wolfram.com/HermitesInterpolatingPolynomial.html]. Look in depth through this online publication to gather further definitions. — Steffen Jaeschke, Sep 27 '20 at 20:38

score -1 · Answer 1 · answered Sep 28 '20 at 15:53

From this reference : Hermite interpolation I get the formula:

Put in Your figures from the table:

I get for the third derivative K==3, each time 0. So the interpolation is already exact!

0 (x - 0)^0 * (x - 1)^1 * (x - 2)^0 == 0 (x-1) == 0

The problem is that

H[x]==x (1 + x)

has the derivative

H'[x]==1 + 2 x

and this has the value H'1==3 <>1.

The solution can be that the third row in the table indicates left-hand-side derivatives in the sense of difference quotient. Then everything fits fine.

linterp = ListInterpolation[yc, xc, InterpolationOrder -> 2]

ListPlot@linterp

How to calculate the expression of error truncation function?

1 Answers1

Linked