4

I am trying to solve a set of ODE's with switching. I implemented using WhenEvents.

xd = {1/√6, √5/√6};
x0 = {1/√2, 1/√2};
min = -0.0001;
max = 0.0001;
tmax = 10;
sol = NDSolve[{
   x1'[t] == -x2[t]*u1[t],
   x2'[t] == x1[t]*u1[t],
   WhenEvent[xd[[1]]* x2[t] - xd[[2]] x1[t] > max, u1[t] -> -1],
   WhenEvent[xd[[1]]* x2[t] - xd[[2]] x1[t] < min, u1[t] -> 1],
   x1[0] == x0[[1]], x2[0] == x0[[2]], u1[0] == -1},
  {x1, x2, x3, u1}, {t, 0, tmax}, DiscreteVariables -> {u1}]
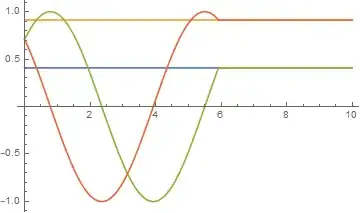
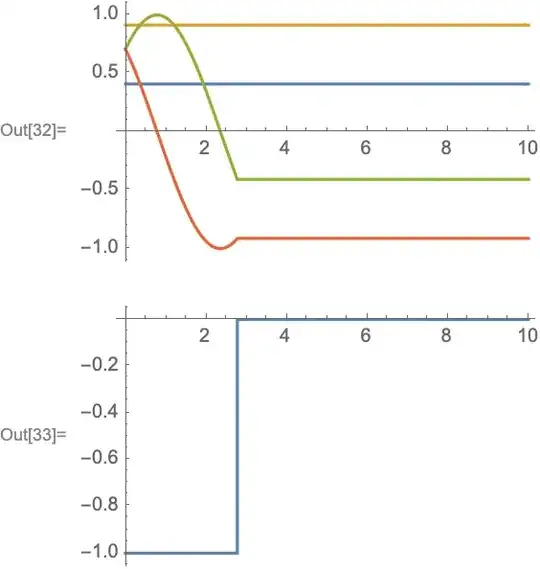
Plot[{xd[[1]], xd[[2]], x1[t] /. sol, x2[t] /. sol}, {t, 0, tmax}, 
 PlotPoints -> 10000]
Plot[u1[t] /. sol, {t, 0, tmax}, PlotPoints -> 10000]

It performs as intended!

How ever, I need to another event WhenEvent[ xd[[1]]* x2[t] - xd[[2]] x1[t] < max && xd[[1]]* x2[t] - xd[[2]] x1[t] > min, u1[t] -> 0], it takes hours and does not produce results.

I think, the last event is raising too many events, so it's taking a lot of time. Is there a work around for this?

A little mouse on the pampas
  • 5,760
  • 2
  • 13
  • 40
kosa
  • 485
  • 2
  • 10
  • I think it's just the new event; try it as the only event. Possibly related: https://mathematica.stackexchange.com/a/39393/4999 – Michael E2 Sep 20 '20 at 21:41
  • Perhaps WhenEvent[Null; <ineq.>, u1[t] -> 0] from my answer in the link does what you want? – Michael E2 Sep 20 '20 at 21:55
  • @MichaelE2 No, it did not work. For f(x)>eps, f(x)<-eps it works. I want to include the event -eps<f(x)<eps. – kosa Sep 20 '20 at 23:30
  • 1
    @MichaelE2 I checked it. I think it's not related to my issue. – kosa Sep 20 '20 at 23:31
  • 1
    Thanks for the accept! This might be worth reporting to Wolfram. I might not be considered a bug, but I think they would want the behavior to be a bit better here. I suspect the algorithm could be improved. – Michael E2 Sep 21 '20 at 05:27
  • @MichaelE2 Thanks for the Help. Yeah, maybe we can submit this. – kosa Sep 21 '20 at 05:30

1 Answers1

5

It seems to be related to the event location method. I used foo to indicate when an event was detected, and murf to show when a step is taken. With the default "LocationMethod", the integration gets stuck on the first event. This happens even when the other two events are removed. It also happens only if the event action is u[t] -> 0; change it to another nonzero value, and everything works fine. (I guess this makes sense. NDSolve is trying to find where the event occurs, but each time it steps across the event, the system stops moving, since u[t] == 0 sets all derivatives equal to zero. I guess that's confusing the root-finding algorithm.)

foo = murf = 0.;
PrintTemporary@
  Dynamic@{foo, Style[murf, PrintPrecision -> 17], Clock@Infinity};
xd = {1/√6, √5/√6};
x0 = {1/√2, 1/√2};
min = -0.0001;
max = 0.0001;
tmax = 10;
sol = NDSolve[{x1'[t] == -x2[t]*u1[t], x2'[t] == x1[t]*u1[t],
   WhenEvent[
    xd[[1]]*x2[t] - xd[[2]] x1[t] > min && 
     xd[[1]]*x2[t] - xd[[2]] x1[t] < max,
    foo = t; u1[t] -> 0, "LocationMethod" -> "LinearInterpolation"],
   WhenEvent[xd[[1]]*x2[t] - xd[[2]] x1[t] > max,(*foo=t;*)
    u1[t] -> -1],
   WhenEvent[xd[[1]]*x2[t] - xd[[2]] x1[t] < min,(*foo=t;*)u1[t] -> 1],
   x1[0] == x0[[1]], x2[0] == x0[[2]], u1[0] == -1},
  {x1, x2, x3, u1}, {t, 0, tmax}, 
  DiscreteVariables -> {u1 ∈ {-1, 0, 1}}, 
  StepMonitor :> (murf = t), MaxSteps -> 1000]

Of course it's stops pretty soon:

Plot[{xd[[1]], xd[[2]], x1[t] /. sol, x2[t] /. sol}, {t, 0, tmax}]
Plot[u1[t] /. sol, {t, 0, tmax}, PlotPoints -> 100]

enter image description here

Michael E2
  • 235,386
  • 17
  • 334
  • 747