Having taken the time to check details on how to do this, I guess I should show it.
We start with the graph.
edges = {1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 3,
1 \[UndirectedEdge] 4, 2 \[UndirectedEdge] 5,
2 \[UndirectedEdge] 6, 5 \[UndirectedEdge] 6,
3 \[UndirectedEdge] 4, 3 \[UndirectedEdge] 7,
6 \[UndirectedEdge] 7, 7 \[UndirectedEdge] 8,
2 \[UndirectedEdge] 9};
verts = Union[Flatten[edges /. UndirectedEdge -> List]];
ew = {1 \[UndirectedEdge] 2 -> 49.6, 1 \[UndirectedEdge] 3 -> 74.4,
1 \[UndirectedEdge] 4 -> 49.6, 2 \[UndirectedEdge] 5 -> 37.2,
2 \[UndirectedEdge] 6 -> 74.4, 5 \[UndirectedEdge] 6 -> 49.6,
3 \[UndirectedEdge] 4 -> 37.2, 3 \[UndirectedEdge] 7 -> 24.8,
6 \[UndirectedEdge] 7 -> 62, 7 \[UndirectedEdge] 8 -> 37.2,
2 \[UndirectedEdge] 9 -> 24.8};
graph = Graph[verts, edges, EdgeWeight -> ew,
VertexLabels -> Placed["Name", Center],
EdgeLabels -> {e_ :> Placed["EdgeWeight", Center]},
VertexSize -> .3, VertexStyle -> Red]
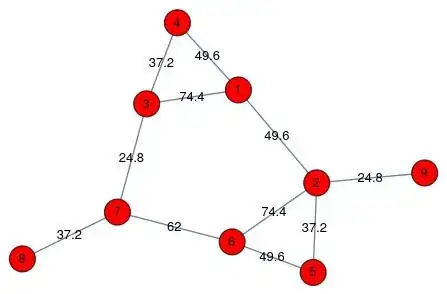
This is not dreadful, as automatic layouts go. And one can improve "by eye" (I do not know why the automated method falls short here). Instead I'll show what I had in mind using multidimensional scaling.
Now we compute the distance matrix.
dmat = GraphDistanceMatrix[graph]
(* Out[1682]= {{0., 49.6, 74.4, 49.6, 86.8, 124., 99.2, 136.4,
74.4}, {49.6, 0., 124., 99.2, 37.2, 74.4, 136.4, 173.6,
24.8}, {74.4, 124., 0., 37.2, 136.4, 86.8, 24.8, 62., 148.8}, {49.6,
99.2, 37.2, 0., 136.4, 124., 62., 99.2, 124.}, {86.8, 37.2, 136.4,
136.4, 0., 49.6, 111.6, 148.8, 62.}, {124., 74.4, 86.8, 124., 49.6,
0., 62., 99.2, 99.2}, {99.2, 136.4, 24.8, 62., 111.6, 62., 0., 37.2,
161.2}, {136.4, 173.6, 62., 99.2, 148.8, 99.2, 37.2, 0.,
198.4}, {74.4, 24.8, 148.8, 124., 62., 99.2, 161.2, 198.4, 0.}} *)
Here is what I had in mind for modifying implementation code of ResourceFunction["MultidimensionalScaling"].
DistanceMatrixDimensionReduce[(dmat_)?MatrixQ, dim_ : 2] :=
With[{len = Length[dmat]},
Module[{diffs, dist2mat, onevec, hmat, bmat, uu, ww, vv},
onevec = ConstantArray[{1}, len];
hmat = IdentityMatrix[len] - onevec . Transpose[onevec]/len;
dist2mat = -dmat/2;
bmat = hmat . dist2mat . hmat; {uu, ww, vv} =
SingularValueDecomposition[bmat, dim]; uu . Sqrt[ww]] /;
dim <= Length[dmat[[1]]] && MatchQ[Flatten[dmat], {_Real ..}]]
We use this to obtain new vertex coordinates for the graph.
newcoords = DistanceMatrixDimensionReduce[dmat]
(* Out[1675]= {{-1.67377, 4.63647}, {-5.6866, 0.575728},
{4.71118, 1.7079}, {2.55599, 4.83333}, {-4.47255, -3.45886},
{-0.471663, -5.30871}, {5.16612, -1.4306},
{6.39076, -2.33059}, {-6.51947, 0.775332}} *)
Now show the new layout.
newLayout =
Graph[verts, edges, VertexCoordinates -> newcoords, EdgeWeight -> ew,
VertexLabels -> Placed["Name", Center],
EdgeLabels -> {e_ :> Placed["EdgeWeight", Center]},
VertexSize -> .3, VertexStyle -> Red]

Can one do better than this? Almost certainly. This method is overly constrained in that it needs all pairwise distances, and it treats them as Euclidean when an actual graph treats them as piecewise Euclidean. So optimizing a sum-of-squares-of-discrepancies will be less constrained. But it might be slow, at least for large graphs.
--- edit ---
Here is a nice way to get a better layout (perfect, in this example). We start from the layout we obtained above and use that to do a local optimization with FindMinumum. For this we require variables to use for the vertex coordinates, and we need the distances to immediate neighbors.
vars = Array[xy, {Length[verts], 2}];
weights = Normal[WeightedAdjacencyMatrix[graph]]
(* Out[1718]= {{0, 49.6, 74.4, 49.6, 0, 0, 0, 0, 0}, {49.6, 0, 0, 0,
37.2, 74.4, 0, 0, 24.8}, {74.4, 0, 0, 37.2, 0, 0, 24.8, 0,
0}, {49.6, 0, 37.2, 0, 0, 0, 0, 0, 0}, {0, 37.2, 0, 0, 0, 49.6, 0,
0, 0}, {0, 74.4, 0, 0, 49.6, 0, 62, 0, 0}, {0, 0, 24.8, 0, 0, 62, 0,
37.2, 0}, {0, 0, 0, 0, 0, 0, 37.2, 0, 0}, {0, 24.8, 0, 0, 0, 0, 0,
0, 0}} *)
Now we create the objective as a sum of squares of discrepancies between symbolic variable distances and graph distances. I use squared distances here to avoid square roots.
objective =
Sum[If[weights[[i, j]] >
0, ((vars[[i]] - vars[[j]]).(vars[[i]] - vars[[j]]) -
weights[[i, j]]^2)^2, 0], {i, Length[weights] - 1}, {j, i + 1,
Length[weights]}]
(* Out[1751]= (-2460.16 + (xy[1, 1] - xy[2, 1])^2 + (xy[1, 2] -
xy[2, 2])^2)^2 + (-5535.36 + (xy[1, 1] -
xy[3, 1])^2 + (xy[1, 2] -
xy[3, 2])^2)^2 + (-2460.16 + (xy[1, 1] -
xy[4, 1])^2 + (xy[1, 2] -
xy[4, 2])^2)^2 + (-1383.84 + (xy[3, 1] -
xy[4, 1])^2 + (xy[3, 2] -
xy[4, 2])^2)^2 + (-1383.84 + (xy[2, 1] -
xy[5, 1])^2 + (xy[2, 2] -
xy[5, 2])^2)^2 + (-5535.36 + (xy[2, 1] -
xy[6, 1])^2 + (xy[2, 2] -
xy[6, 2])^2)^2 + (-2460.16 + (xy[5, 1] -
xy[6, 1])^2 + (xy[5, 2] - xy[6, 2])^2)^2 + (-615.04 + (xy[3, 1] -
xy[7, 1])^2 + (xy[3, 2] - xy[7, 2])^2)^2 + (-3844 + (xy[6, 1] -
xy[7, 1])^2 + (xy[6, 2] -
xy[7, 2])^2)^2 + (-1383.84 + (xy[7, 1] -
xy[8, 1])^2 + (xy[7, 2] - xy[8, 2])^2)^2 + (-615.04 + (xy[2, 1] -
xy[9, 1])^2 + (xy[2, 2] - xy[9, 2])^2)^2 *)
Optimize this.
{min, vals} =
FindMinimum[objective,
Flatten[MapThread[List, {vars, newcoords}, 2], 1]]
(* Out[1761]= {1.485310^-24, {xy[1, 1] -> -23.2827, xy[1, 2] -> 42.3923,
xy[2, 1] -> -42.4665, xy[2, 2] -> -3.34769, xy[3, 1] -> 25.6614,
xy[3, 2] -> -13.6419, xy[4, 1] -> 22.5485, xy[4, 2] -> 23.4276,
xy[5, 1] -> -5.29537, xy[5, 2] -> -4.81353, xy[6, 1] -> 15.6832,
xy[6, 2] -> -49.7586, xy[7, 1] -> 27.6269, xy[7, 2] -> 11.0801,
xy[8, 1] -> 0.512013, xy[8, 2] -> -14.388, xy[9, 1] -> -20.9875,
xy[9, 2] -> 9.04959}} )
Use this to create the new layout.
newercoords = vars /. vals;
vcoords3 = MapIndexed[#2[[1]] -> # &, newercoords];
newLayout =
Graph[verts, edges, VertexCoordinates -> vcoords3, EdgeWeight -> ew,
VertexLabels -> Placed["Name", Center],
EdgeLabels -> {e_ :> Placed["EdgeWeight", Center]},
VertexSize -> .3, VertexStyle -> Red]

Not terribly pretty but it seems to respect the distance requirements. One can obtain different solutions by specifying a Method option to FindMinimum. (For reasons unknown to me, "LevenbergMarquardt" balks at this objective function. It wants an explicit sum of squares. Whhich I gave it. Go figure.)
Actual graph layout functions tend to add penalties to move vertices apart, so one might in principle get a better looking layout while still satisfying the distance requirements. Offhand I am not familiar with the specifics. Roughly, one such method applies a spring-like force in its penalty function. This is getting outside of my expertise and also a bit beyond the question that was asked.
--- end edit ---



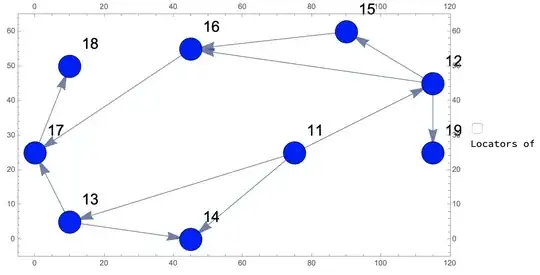
{110, 34, 102}with weights{24.8, 62., 24.8}. – Szabolcs Sep 22 '20 at 09:41ResourceFunction["MultidimensionalScaling"]to relocate the vertices in R^2. If you are dead set on using a different optimization, go withFindMinimumoverMinimize. – Daniel Lichtblau Sep 24 '20 at 17:49use an all-pairs-shortest-paths to get the pair-wise distance matrix. Then crib code from e.g. ResourceFunction["MultidimensionalScaling"] to relocate the vertices in R^2.? – Natasha Sep 25 '20 at 13:29GraphDistanceMatrixcan be used for this purpose. – Daniel Lichtblau Sep 25 '20 at 15:25