Triangle mapped on a sphere in $\mathbb R^3$?

Question

How can I map a triangle on a sphere? I want to visualize (plot or animate) it for my student in Non-Euclidean geometry. I have no restrictions on the triangle's kind or on the sphere in $\mathbb R^3$. Thanks for any hint.

Answer 1

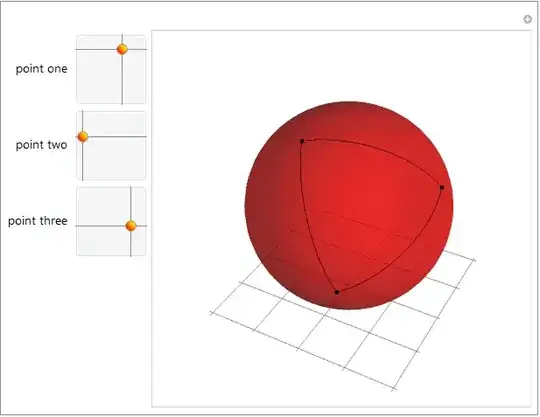
In the comments J. M. linked to a Demonstration by Borut Levart.

Here is code from that, with my own refactoring:

eps = 10^-6;

(* from spherical to cartesian coordinates *)
sp[{ϕ_, θ_}] := {Sin[θ]*Cos[ϕ], Sin[θ]*Sin[ϕ], Cos[θ]}

(* part of great circle between two sphere points *)
ark[{r1_, r2_}, nt_] := Table[
  RotationTransform[t VectorAngle[r1, r2],
    Cross[r1, r2]][r1], {t, 0, 1, 1/nt}]

Manipulate[
 If[p1 == p2, p1 = .99 p2];
 If[p1 == p3, p1 = .99 p3];
 If[p3 == p2, p3 = .98 p2];
 Graphics3D[{
   {Red, Opacity[.6], Sphere[{0, 0, 0}, .995]},
   ark[#, 20] & /@ Subsets[sp /@ {p1, p2, p3}, {2}] // Line,
   PointSize[.015], Point[sp /@ {p1, p2, p3}]
  },
  Boxed -> False,
  ImageSize -> {400, 400},
  FaceGrids -> {{0, 0, -1}},
  FaceGridsStyle -> GrayLevel[.5]
 ],
 {{p1, {4.2, .5}, "point one"}, {eps, π (1 - eps)}, {2 π (1 - eps), eps}},
 {{p2, {.1, 1.1}, "point two"}, {eps, π (1 - eps)}, {2 π (1 - eps), eps}},
 {{p3, {5.1, 1.8}, "point three"}, {eps, π (1 - eps)}, {2 π (1 - eps), eps}},
 ControlPlacement -> Left, SaveDefinitions -> True
]

Answer 2

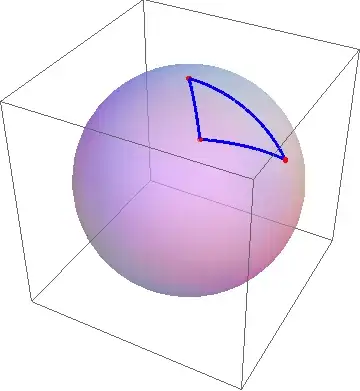
I might as well... let me present here the spherical geometry version of this answer. I shall provide two flavors in this answer as well: one where all the arc lengths are given, and one where all the interior angles are given. The formulae used within those routines are nothing more than an application of the spherical law of cosines.

Now, on to the routines. But first, a few auxiliaries:

sphericalDistance[{u1_, v1_}, {u2_, v2_}] :=
                  InverseHaversine[Haversine[v1 - v2] + Sin[v1] Sin[v2] Haversine[u1 - u2]]

GreatCircleArc[p1_, p2_] := Module[{cc, sp1, sp2},
       cc = Cos[sphericalDistance[p1, p2]/2];
       {sp1, sp2} = Append[Sin[#2] Through[{Cos, Sin}[#1]], Cos[#2]] & @@@ {p1, p2};
       BSplineCurve[{sp1, Normalize[(sp1 + sp2)/2]/cc, sp2}, SplineDegree -> 2,
                    SplineKnots -> {0, 0, 0, 1, 1, 1}, SplineWeights -> {1, cc, 1}]]

Here, then, is the routine for drawing a spherical triangle on a unit sphere, given the (normalized) side lengths:

With[{a = π/5, b = π/4, c = π/3},
     Block[{β = N[ArcCos[(Cos[b] - Cos[a] Cos[c])/(Sin[a] Sin[c])]]}, 
      Graphics3D[{{Opacity[1/2], Sphere[]},
                  {Directive[Red, AbsolutePointSize[6]], 
                   Point[{{0, 0, 1}, {Sin[c], 0, Cos[c]},
                          {Sin[a] Cos[β], -Sin[a] Sin[β], Cos[a]}}]},
                  {Directive[Blue, AbsoluteThickness[3]],
                   GreatCircleArc @@@ Partition[{{0, 0}, {0, c}, {-β, a}}, 2, 1, 1]}},
                 PlotRange -> ConstantArray[{-1, 1}, 3]]]]

Here's the routine for drawing a spherical triangle on the unit sphere, given the interior angles:

With[{α = π/4, β = π/3, γ = π/2},
 Block[{a, c},
  {a, c} = N[ArcCos[{(Cos[α] + Cos[β] Cos[γ])/(Sin[β] Sin[γ]),
                      (Cos[γ] + Cos[α] Cos[β])/(Sin[α] Sin[β])}]]; 
  Graphics3D[{{Opacity[1/2], Sphere[]},
              {Directive[Red, AbsolutePointSize[6]], 
               Point[{{0, 0, 1}, {Sin[c], 0, Cos[c]},
                      {Sin[a] Cos[β], -Sin[a] Sin[β], Cos[a]}}]},
              {Directive[Blue, AbsoluteThickness[3]],
               GreatCircleArc @@@ Partition[{{0, 0}, {0, c}, {-β, a}}, 2, 1, 1]}}, 
             PlotRange -> ConstantArray[{-1, 1}, 3]]]]

I made the normalization that one of the vertices is always $(\theta,\varphi)=(0,0)$; if you want your triangles to be positioned somewhere else, modifying the routines should not be too difficult.