Quickest way to test whether array is constant

Question

At the moment I use Length[ DeleteDuplicates[ array ] ] == 1 to check whether an array is constant, but I'm not sure whether this is optimal.

What would be the quickest way to test whether an array consists of equal elements?

What if the elements would be integers?

What if they are floats?

Your Length[ DeleteDuplicates[ array ] ] == 1 does not test whether array is constant but rather whether its rows are equal. This is equivalent to Equal @@ array. To test whether array is constant you could use Equal @@ Flatten[array] — Bob Hanlon, Sep 29 '20 at 14:00
@Henrik has a good idea but "duplicate" and "equal" mean different things in Mathematica, especially for floating-point numbers and expressions like array = {1 + Sqrt[3], Sqrt[4 + 2 Sqrt[3]]}. An alternative to check duplicates is 0 == Subtract @@ MinMax[array]. — Michael E2, Sep 29 '20 at 14:29
@MichaelE2 Good point. Admittedly, I had only the (machine) integer case in mind. — Henrik Schumacher, Sep 29 '20 at 14:46
What is the maximum depth of your arrays? Length[DeleteDuplicates[array]] assumes it's depth 1 (a "flat" or non-nested list). MinMax[array] will work with arrays of any depth (vectors, matrices, tensors...). — Michael E2, Sep 29 '20 at 15:07
@HenrikSchumacher I suspect the OP neglected the point because of the use of DeleteDuplicates and the question about "equal elements." I raised it, so that OP might clarify which criterion is desired. (One might want to use Chop or Threshold on max - min in the case of floats depending on how array is calculated.) — Michael E2, Sep 29 '20 at 15:13
@HenrikSchumacher You should add the MinMax approach as an answer, it is faster than the other answers. — Carl Woll, Sep 29 '20 at 15:41

Sjoerd Smit · Accepted Answer · 2020-09-29T15:23:39.710

Here are two methods that are quite fast for flat lists (you can flatten arrays to test at deeper levels):

const = ConstantArray[1, 100000];
nonconst = Append[const, 2];

Using CountDistinct (or CountDistinctBy):

CountDistinct[const] === 1
CountDistinct[nonconst] === 1

True

False

Based on pattern matching:

MatchQ[const, {Repeated[x_]}]
MatchQ[nonconst , {Repeated[x_]}]

True

False

The MatchQ approach can be generalized for deeper arrays using Level without having to Flatten everything:

constTensor = ConstantArray[1, {5, 5, 5}];
MatchQ[Level[constTensor, {ArrayDepth[constTensor]}], {Repeated[x_]}]

True

Level doesn't always perform better than Flatten, though. Flatten seems very efficient for packed arrays.

Timings

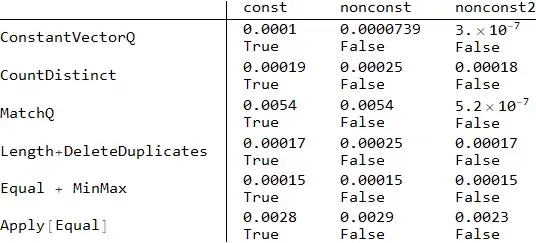
CountDistinct[const] // RepeatedTiming
MatchQ[const, {Repeated[x_]}] // RepeatedTiming

{0.00021, 1}

{0.0051, True}

MatchQ has the advantage that it short-circuits when a list doesn't match:

nonconst2 = Prepend[const, 2];
MatchQ[nonconst2, {Repeated[x_]}] // RepeatedTiming

{6.*10^-7, False}

Edit

Here's another method I just came up with. It avoids messing around with the array (flattening etc.):

constantArrayQ[arr_] := Block[{
   depth = ArrayDepth[arr],
   fst
  },
   fst = Extract[arr, ConstantArray[1, depth]];
   FreeQ[arr, Except[fst], {depth}, Heads -> False]
];

It seems like this one is quite fast for unpacked arrays:

constTensor = ConstantArray[1, 400*{1, 1, 1}];
constTensor[[1, 1, 1]] = 2.;
<< Developer`
PackedArrayQ @ constTensor
(* False *)
MatchQ[Level[constTensor, {ArrayDepth[constTensor]}], {Repeated[x_]}] // AbsoluteTiming
MatchQ[Flatten[constTensor], {Repeated[x_]}] // AbsoluteTiming
constantArrayQ[constTensor] // AbsoluteTiming
(* {2.54311, False} )
( {2.20663, False} )
( {0.0236709, False} *)

For packed arrays, it looks like MatchQ[Flatten[constTensor], {Repeated[x_]}] is actually the fastest:

constTensor = ConstantArray[1, 400*{1, 1, 1}];
constTensor[[1, 1, 1]] = 2;
<< Developer`
PackedArrayQ @ constTensor
(* True *)
MatchQ[Level[constTensor, {ArrayDepth[constTensor]}], {Repeated[x_]}] // AbsoluteTiming
MatchQ[Flatten[constTensor], {Repeated[x_]}] // AbsoluteTiming
constantArrayQ[constTensor] // AbsoluteTiming
(* {2.76109, False} )
( {0.19088, False} )
( {1.17001, False} *)

Unexpectedly, MatchQ doesn't check the last bit on machine floats: MatchQ[Table[1. + k*$MachineEpsilon, {k, 2}], {Repeated[x_]}]. Timings? — Michael E2, Sep 29 '20 at 14:30

kglr · Answer 2 · 2020-09-29T17:31:08.993

9

Statistics`Library`ConstantVectorQ is quite fast.

Using Sjoerd's input examples:

const = ConstantArray[1, 100000];
nonconst = Append[const, 2];
nonconst2 = Prepend[const, 2];
t11 = StatisticsLibraryConstantVectorQ@const // RepeatedTiming;
t21 = CountDistinct[const] == 1 // RepeatedTiming;
t31 = MatchQ[const, {Repeated[x_]}] // RepeatedTiming;
t41 = Length[DeleteDuplicates@const] == 1 // RepeatedTiming;
t51 = Equal @@ MinMax[const] // RepeatedTiming;
t61 = Equal @@ const // RepeatedTiming;
t12 = StatisticsLibraryConstantVectorQ@nonconst // RepeatedTiming
t22 = CountDistinct[nonconst] == 1 // RepeatedTiming;
t32 = MatchQ[nonconst, {Repeated[x_]}] // RepeatedTiming;
t42 = Length[DeleteDuplicates@nonconst] == 1 // RepeatedTiming;
t52 = Equal @@ MinMax[nonconst] // RepeatedTiming;
t62 = Equal @@ nonconst // RepeatedTiming;
t13 = StatisticsLibraryConstantVectorQ@nonconst2 // RepeatedTiming
t23 = CountDistinct[nonconst2] == 1 // RepeatedTiming;
t33 = MatchQ[nonconst2, {Repeated[x_]}] // RepeatedTiming;
t43 = Length[DeleteDuplicates@nonconst2] == 1 // RepeatedTiming;
t53 = Equal @@ MinMax[nonconst2] // RepeatedTiming;
t63 = Equal @@ nonconst2 // RepeatedTiming;
TableForm[{{t11, t12, t13}, {t21, t22, t23}, {t31, t32, t33}, {t41, 
   t42, t43}, {t51, t52, t53}, {t61, t62, t63}}, 
 TableHeadings -> {{"ConstantVectorQ", "CountDistinct", "MatchQ", 
    "Length+DeleteDuplicates", "Equal + MinMax", "Apply[Equal]"}, 
    {"const", "nonconst", "nonconst2"}}]

edited Sep 29 '20 at 17:31

answered Sep 29 '20 at 15:08

kglr

394,356
18
477
896

3

I don't know who wrote Statistics`Library but it's full of good stuff. (+1) – Michael E2 Sep 29 '20 at 15:18
Why is CountDistinct@const so much faster than Equal@@const or SameQ@@const? That seems counterintutive. – Alan Sep 29 '20 at 16:40
Oh, nice find there – Sjoerd Smit Sep 29 '20 at 17:07
2

@Alan It's because the array is "unpacked". Start with const = Developer`FromPackedArray@ConstantArray[1, 100000]; and rerun the timings; then Equal @@ const is only about twice as slow. See What is a packed array? – Michael E2 Sep 29 '20 at 17:11
@Alan, the difference may also have to do with the fact that CountDistinct uses Length[DeleteDuplicates @ const] == 1 under the hood. – kglr Sep 29 '20 at 17:34
2

@kglr This still seems odd to me. DeleteDuplicates should require comparison and deletion, while SameQ should only require comparison. Perhaps SameQ is doing all pairwise comparisons in order not to assume transitivity of the comparisons? – Alan Sep 29 '20 at 18:21
3

@Alan SameQ @@ array is a little faster than DeleteDuplicates[array] on array = Sqrt@ConstantArray[2, {100000}];. The reason DeleteDuplicates is faster on array = ConstantArray[2, {100000}]; is that in effect it computes DeleteDuplicates[Developer`ToPackedArray@array] and SameQ @@ array cannot take advantage of packed arrays. Numbers have certain optimizations available that general expressions do not. Data functions such as DeleteDuplicates are programmed to take advantage of them. – Michael E2 Sep 30 '20 at 02:44
@MichaelE2 OK, that makes sense. Clearly I've paid too little attention to when arrays are packed and unpacked. Can you recommend useful documentation? – Alan Sep 30 '20 at 18:16
1

@Alan The Q&A I linked is probably the best discussion available. The closest to official documentation is this Wolfram Library notebook and article by one of the lead kernel developers, https://library.wolfram.com/infocenter/Demos/391/, which is also linked in a comment to that Q&A. – Michael E2 Sep 30 '20 at 18:35

score 6 · Answer 3 · answered Sep 29 '20 at 16:45

6

Equal@@MinMax[array] might be quite fast if array is a packed list of integers. But it cannot short-circuit like Statistics`Library`ConstantVectorQ does. And it is also not very robust with regard to (machine) floating point numbers: Equal and SameQ both use a certain tolerance for their equality checks (I forgot which precise one they use; I just recall that the tolerance of SameQ should be the lower one). This may or may not be the desired behavior in a particular application.

answered Sep 29 '20 at 16:45

Henrik Schumacher

106,770
7
179
309

1

The tolerances are Internal`$EqualTolerance and Internal`$SameQTolerance for those who wish to change them. For example, Block[{Internal`$EqualTolerance = 0}, Equal @@ MinMax[array]]. – Michael E2 Sep 29 '20 at 17:07

Quickest way to test whether array is constant

3 Answers3

Timings

Edit

Linked